1. 神经网络

1.1. 感知器

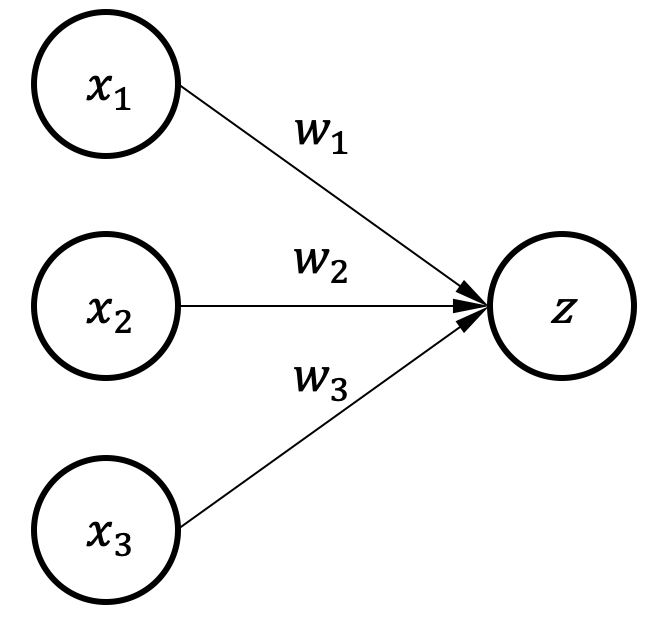
图1.1.1 有三个输入和单一输出的神经元

图1.1.1是一个神经元的例子，输入数据\(x\)根据连线上的权重\(w\)做加权求和得到输出\(z\)，我们把这样的模型叫作感知器（Perceptron）。 因为输入和输出之间只有一层神经连接，这个模型也叫做单层感知器。 图1.1.1的模型计算可以写为：\(z = w_{1}x_{1}+ w_{2}x_{2} + w_{3}x_{3}\)。

当输入数据用列向量\({x}=[x_1,x_2,x_3]^T\)表示，模型权重用行向量\({w}=[w_1,w_2,w_3]\)表示，那么输出的标量\(z\)可以写为：

(1.1.1)\[\begin{split}z = \begin{bmatrix} w_1,w_2,w_3\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} ={w}{x}\end{split}\]

我们可以利用输出标量\(z\)为输入的加权组合来实现特定任务。 比如，可以对“好苹果”和“坏苹果”进行分类，输入的\(x_1,x_2,x_3\)分别代表三种不同的特征：1）红色的程度，2）有没有洞，3）大小。如果苹果的大小对这个判断没有影响，那么对应的权重就为零。 这个神经网络的训练，其实就是选择合适的权重，来实现我们的任务。比如我们可以选择合适的权重，使得当\(z\)小于等于\(0\)时代表“坏苹果”，而当\(z\)大于\(0\)时则是“好苹果”。 则最终的分类输出标签\(y\)如下，为\(1\)时代表好，\(0\)代表坏。这个神经元的输入和输出之间只有一层，所以可以成为单层神经网络。

(1.1.2)\[\begin{split}y = \begin{cases} 1 & z>0 \\ 0 & z \leq 0 \\ \end{cases}\end{split}\]

1.2. 决策边界vs.偏置

通过选择合适的权重以\(z\)大于或小于\(0\)来对输入数据做分类的话，可以在数据空间上获得一个决策边界 （Decision Boundary）。如 图1.2.1所示，以神经元输出\(z=0\)作为输出标签\(y\)的决策边界， 没有偏置时决策边界必然经过坐标原点，如果数据样本点不以原点来分开，会导致分类错误。 为了解决这个问题，可以在神经元上加入一个偏置（Bias）。 图1.2.2 是一个有偏置\(b\)的神经元模型，可以用 (1.2.1)表达：

(1.2.1)\[z = w_{1}x_{1}+ w_{2}x_{2}+ w_{3}x_{3} + b\]

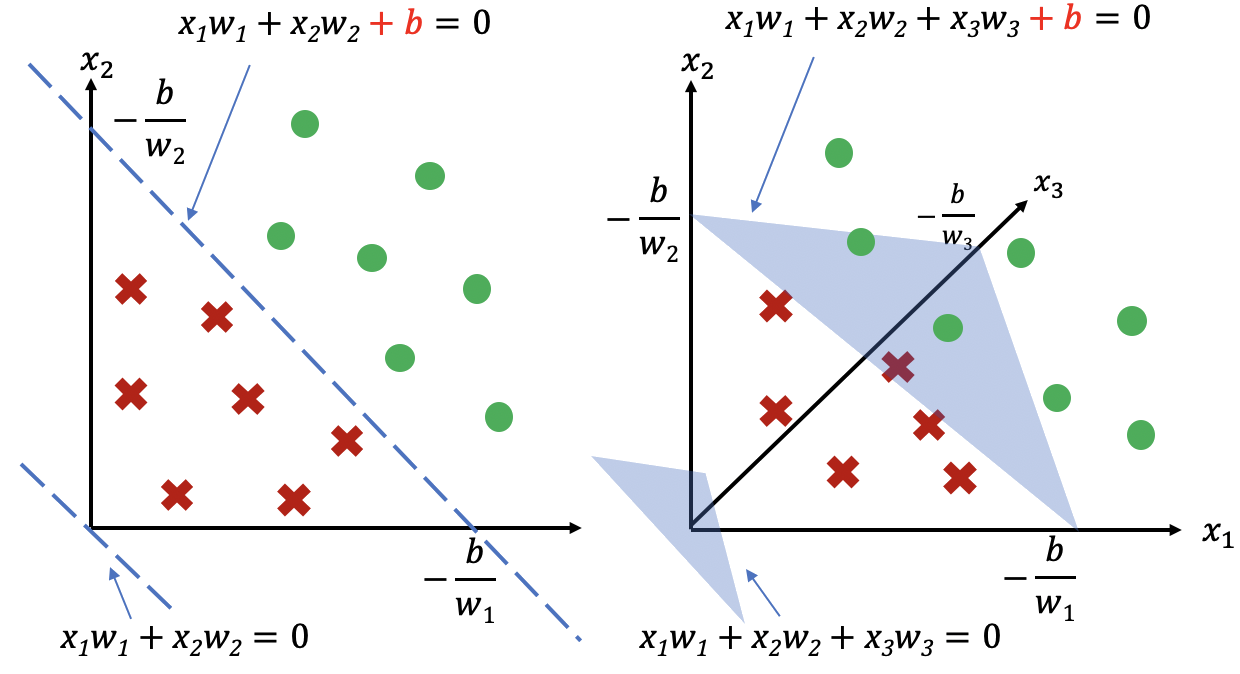
图1.2.1 两个输入（左）和三个输入（右）时的决策边界。不同形状的点代表不同类别的数据，需要找到\(z=0\)作为决策边界来把不同数据点分开。两个输入时决策边界是一直线，三个输入时决策边界是一个平面，高维度输入时决策边界称为超平面（Hyperplane）。 左： \(z=w_{1}x_{1}+w_{2}x_{2}+b\)。右：\(z=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b\)。没有偏置时，决策边界必然经过原点，所以不能分开不同类别的数据样本。

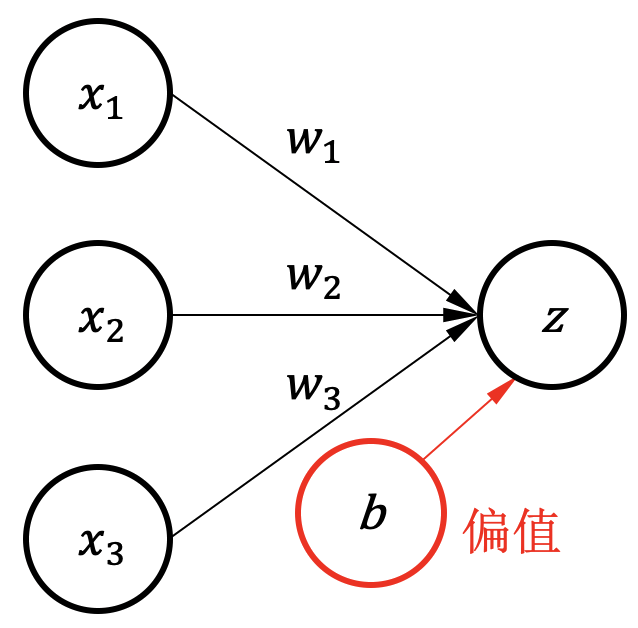
图1.2.2 一个有偏置的单层神经网络

有了偏置以后，决策边界（直线、平面或超平面）可以不经过坐标原点，因此能更好地分类样本。 准确来说，决策边界把这些样本数据分成两个不同的类别，这个边界是 \(\{x_1, x_2, x_3 | w_{1}x_{1}+ w_{2}x_{2}+ w_{3}x_{3} + b = 0\}\)。

1.3. 逻辑回归

上述神经元的输入和输出是线性关系，为了提供非线性的数据表达能力，可以在神经元输出上加上激活函数（Activation Function），最常见的激活函数有Sigmoid、Tanh、ReLU和Softmax等。 比如，上述神经元以\(z=0\)为分界来做分类任务，那么我们可不可以让神经元输出一个概率呢？比如输出\(0~1\)，\(1\)代表输入数据\(100\%\)为某一类。 为了让神经元输出\(0~1\)，可以在\(z\)上加一个逻辑函数Sigmoid， 如 (1.3.1)所示，Sigmoid把数值限制在0和1之中，通过一个简单的临界值（如：0.5）来决定最终输出的标签是否属于某个类别。这个方法叫做逻辑回归（Logistic Regression）。

(1.3.1)\[a = f({z}) = \frac{1}{1+{\rm e}^{-{z}}}\]

1.4. 多个神经元

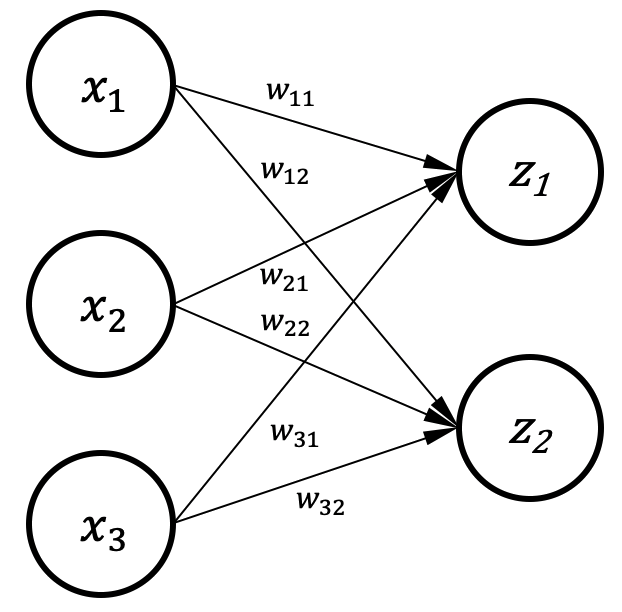
图1.4.1 多个神经元

上述网络只有一个输出，若多个神经元在一起就可以有多个输出。 图1.4.1是有两个输出的网络，每个输出都和所有输入相连，所以也被称全连接层（Fully-Connected(FC) Layer）， 可由下述式子 (1.4.1)表示X。

(1.4.1)\[\begin{split}z_{1} &= w_{11}x_{1} + w_{12}x_{2} + w_{13}x_{3} + b_1 \notag \\ z_{2} &= w_{21}x_{1} + w_{22}x_{2} + w_{23}x_{3} + b_2\end{split}\]

如下式子表示了矩阵方法的实现：

(1.4.2)\[\begin{split}{z} = \begin{bmatrix} z_1 \\ z_2 \end{bmatrix} = \begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} = {W}{x} + {b}\end{split}\]

多输出的网络可以实现多分类问题，比如有10个数值输出，每个数值分别代表一类物品的概率，每个输出在\(0\)到\(1\)之间，10个输出之和为\(1\)。 可用 (1.4.3)的Softmax 函数来实现，\(K\)为输出的个数：

(1.4.3)\[f({z})_{i} = \frac{{\rm e}^{z_{i}}}{\sum_{k=1}^{K}{\rm e}^{z_{k}}}\]

1.5. 多层感知器

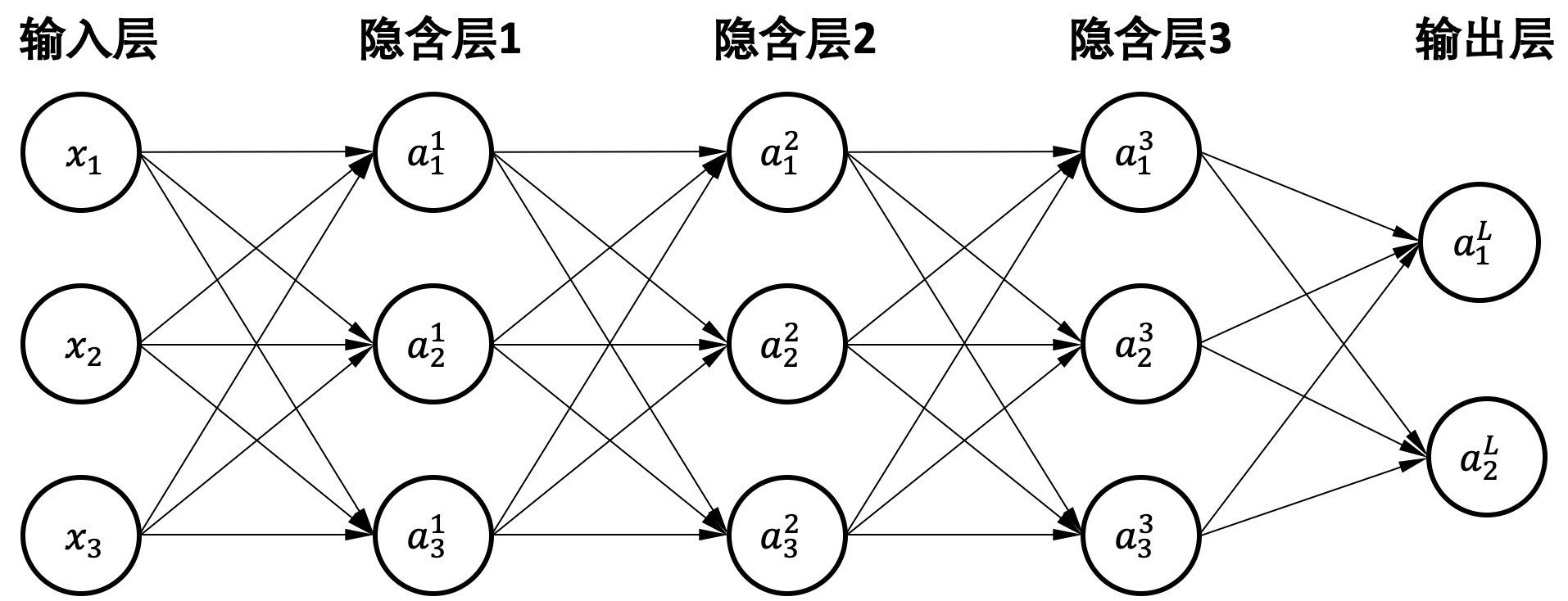
图1.5.1 多层感知器例子。\(a^l_i\)表示神经元输出\(z\)经过激活函数后的值，其中\(l\)代表层的序号（\(L\)代表输出层），\(i\)代表输出的序号

多层感知器（Multi-Layer Perceptron，MLP） [Rosenblatt, 1958]通过叠加多层全连接层来提升网络的表达能力。相比单层网络，多层感知器有很多中间层的输出并不暴露给最终输出，这些层被称为隐含层（Hidden Layers）。这个例子中的网络可以通过下方的串联式矩阵运算实现，其中\(W^l\)和\(b^l\)代表不同层的权重矩阵和偏置，\(l\)代表层号，\(L\)代表输出层。

(1.5.1)\[{z} = f({W^L}f({W^3}f({W^2}f({W^1}{x} + {b^1}) + {b^2}) + {b^3}) + {b^L})\]

在深度学习时代，网络模型基本都是多层的神经网络层连接起来的，输入数据经过多层的特征提取，可以学到不同抽象层级的特征向量（Feature Vector）。下面我们介绍一下其他常用的神经网络层。

1.6. 卷积网络

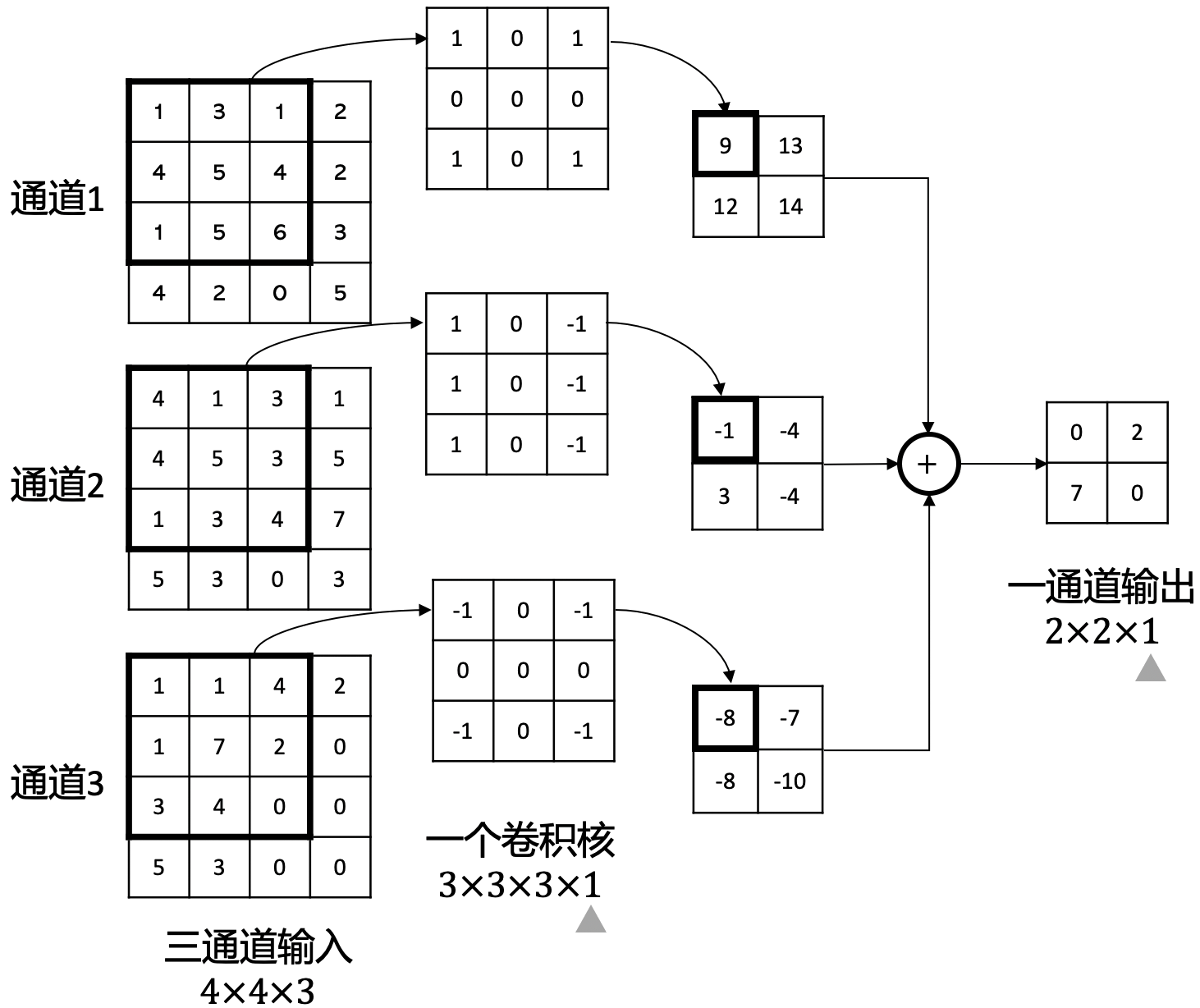
图1.6.1 卷积运算例子。 输入一个三通道的数据，其大小为\(4 \times 4 \times 3\)（高 \(\times\) 宽 \(\times\) 通道数），为了对各个通道做卷积，卷积核也必须有三个通道，一个卷积核的大小为\(3 \times 3 \times 3 \times 1\)（高 \(\times\) 宽\(\times\)输入通道数\(\times\)输出通道数（卷积核的个数））。有多少个卷积核就有多少个输出的特征图（Feature Map），在这个例子中因为只有一个卷积核，所以输出的通道数为1，高宽为2。与此同时，我们把这种高维度的输入数据称为张量（Tensor），比如RGB图像、视频、前一层卷积层的输出等等。

卷积神经网络 （Convolutional Neural Network，CNN） [LeCun et al., 1989]由多层卷积层（Convolutional Layer）组成，常用于计算机视觉任务 [Krizhevsky et al., 2012][He et al., 2016]。 图1.6.1描述了一个卷积运算的例子。 根据卷积的特点，我们可以知道两个事实：1）一个卷积核的通道数，等于输入的通道数；2）输出的通道数，等于卷积核的数量。

图1.6.1例子中，卷积核每次滑动一个数值的范围来进行卷积操作，我们称它的步长（Stride）为1。此外，如果希望输入的边缘数值也能被考虑在内的话，则需要对边缘做填零（Zero Padding）操作。 图1.6.1例子中，如果输入的每个通道上下左右都填充一圈零，那么输出的大小则为\(4\times 4\times 1\)。填零的圈数取决于卷积核的大小，卷积核越大则填零圈数越大。

为了对输入的图像数据做特征提取，卷积核数量往往比输入数据的通道数据要多，这样的话输出数据的数值会很多，计算量变大。然而图像数据中相邻像素的特征往往相似，所以我们可以对相邻的输出特征进行聚合操作。池化层就是为了实现这个目的，我们通常有两种池化方法最大值池化（Max Pooling）和平均值池化（Mean Pooling）。如 图1.6.2所示，假设池化的卷积核高宽为\(2\times2\)，输入\(4\times4\)的数据，步长为2（步长为1时，则输出等于输入），则输出为\(2\times2\)。

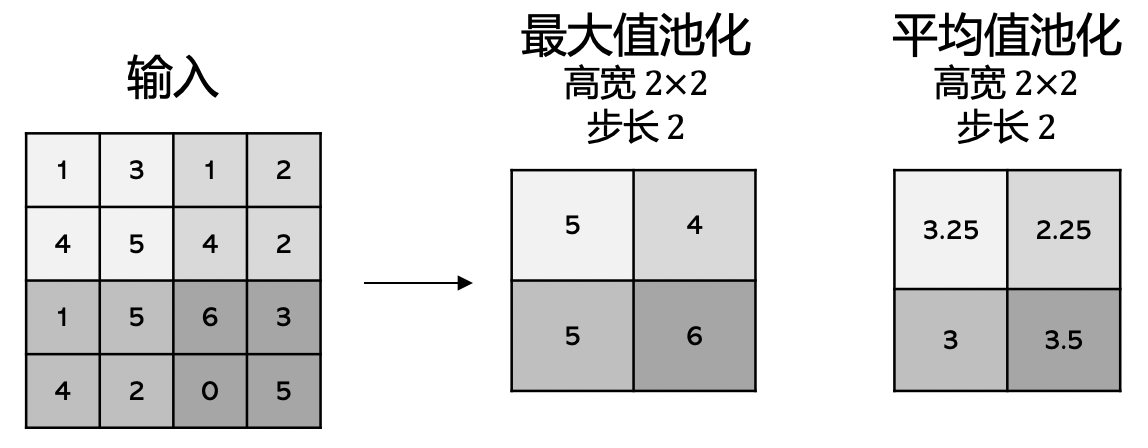
图1.6.2 \(2 \times 2\) 最大值池化和平均值池化的例子，它们的步长为2，输入大小是\(4 \times 4\)

卷积层和全连接层都是很常用的，但是卷积层在输入是高维度的图像时，需要的参数量远远小于全连接层。卷积层的运算和全连接层是类似的，前者基于高维度张量运算，后者基于二维矩阵运算。

1.7. 时序模型

现实生活中除了图像还有大量时间序列数据，例如视频、股票价格等等。循环神经网络（Recurrent Neural Networks，RNN） [Rumelhart et al., 1986]是一种处理序列数据的深度学习模型结构。序列数据是一串连续的数据\(\{x_1, x_2, \dots, x_n\}\)，比如每个\(x\)代表一个句子中的单词。

为了可以接收一连串的输入序列，如 图1.7.1所示，朴素循环神经网络使用了循环单元（Cell）作为计算单元，用隐状态（Hidden State）来存储过去输入的信息。具体来说，对输入模型的每个数据\(x\)，根据公式 (1.7.1)，循环单元会反复计算新的隐状态，用于记录当前和过去输入的信息。而新的隐状态会被用到下一单元的计算中。

(1.7.1)\[{h}_t = {W}[{x}_t; {h}_{t-1}] + {b}\]

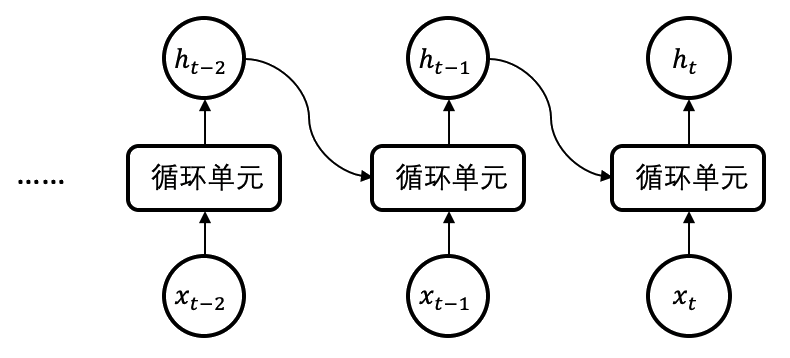
图1.7.1 朴素循环神经网络。 在每一步的计算中，循环单元通过过去时刻的隐状态\({h}_{t-1}\)和当前的输入\({x}_t\)，求得当前的隐状态\({h}_t\)。

然而这种简单的朴素循环神经网络有严重的信息遗忘问题。比如说我们的输入是“我是中国人，我的母语是_”，隐状态记住了”中国人”的信息，使得网络最后可以预测出”中文”一词；但是如果句子很长的时候，隐状态可能记不住太久之前的信息了，比如说”我是中国人，我去英国读书，后来在法国工作，我的母语是_”，这时候在最后的隐状态中关于“中国人”的信息可能会被因为多次的更新而遗忘了。 为了解决这个问题，后面有人提出了各种各样的改进方法，其中最有名的是长短期记忆（Long Short-Term Memory，LSTM） [Hochreiter et al., 1997]。关于时序的模型还有很多很多，比如近年来出现的Transformer [Vaswani et al., 2017]等等。