15.1. 强化学习介绍¶
近年来,强化学习作为机器学习的一个分支受到越来越多的关注。2013 年 DeepMind 公司的研究人员提出了深度 Q 学习 [Mnih et al., 2013](Deep Q-learning),成功让 AI 从图像中学习玩电子游戏。自此以后,以 DeepMind 为首的科研机构推出了像 AlphaGo 围棋 AI 这类的引人瞩目的强化学习成果,并在 2016 年与世界顶级围棋高手李世石的对战中取得了胜利。自那以后,强化学习领域连续取得了一系列成就,如星际争霸游戏智能体 AlphaStar、Dota 2 游戏智能体 OpenAI Five、多人零和博弈德州扑克的 Pluribus、机器狗运动控制算法等。在这一系列科研成就的背后,是整个强化学习领域算法在这些年内快速迭代进步的结果,基于模拟器产生的大量数据使得对数据“饥饿”(Data Hungry)的深度神经网络能够表现出很好的拟合效果,从而将强化学习算法的能力充分发挥出来,在以上领域中达到或者超过人类专家的学习表现。目前,强化学习已经从电子游戏逐步走向更广阔的应用场景,如机器人控制、机械手灵巧操作、能源系统调度、网络负载分配、股票期货交易等一系列更加现实和富有意义的领域,对传统控制方法和启发式决策理论发起冲击。
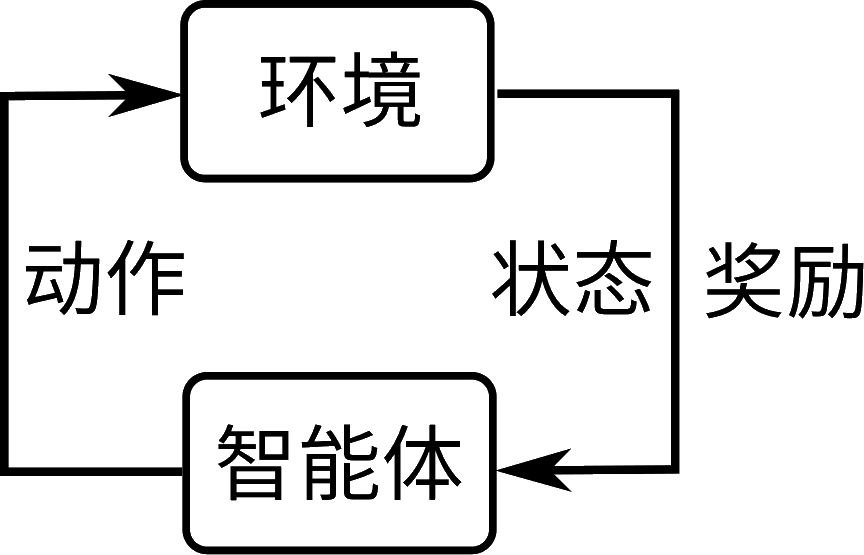
图15.1.1 强化学习框架¶
强化学习的核心是不断地与环境交互来优化策略从而提升奖励的过程,主要表现为基于某个状态(State)下的动作(Action)的选择。进行这一决策的对象我们常称为智能体(Agent),而这一决策的影响将在环境(Environment)中体现。更具体地,不同的决策会影响环境的状态转移(State Transition)和奖励(Reward)。以上状态转移是环境从当前状态转移到下一状态的函数,它可以是确定性也可以是随机性的。奖励是环境对智能体动作的反馈,通常是一个标量。以上过程可以抽象为 图15.1.1所示,这是文献中最常见的强化学习的模型描述。
举例来说,当人在玩某个电子游戏的时候,需要逐渐熟悉游戏的操作以取得更好的游戏结果,那么人从刚接触到这个游戏到逐步掌握游戏技巧的这个过程为一个类似于强化学习的过程。该游戏从开始后的任一时刻,会处于一个特定的状态,而人通过观察这个状态会获得一个观察量(Observation)(如观察游戏机显示屏的图像),并基于这个观察量做出一个操作动作(如发射子弹),这一动作将改变这个游戏下一时刻的状态,使其转移到下一个状态(如把怪物打败了),并且玩家可以知道当前动作的效果(如产生了一个正或负的分数,怪物打败了则获得正分数)。这时玩家再基于下一个状态的观察量做出新的动作选择,周而复始,直到游戏结束。通过反复的操作和观察,人能够逐步掌握这个游戏的技巧,一个强化学习智能体也是如此。
这里注意,有几个比较关键的问题:一是观察量未必等于状态,而通常观察量是状态的函数,从状态到观察量的映射可能有一定的信息损失。对于观察量等于状态或者根据观察量能够完全恢复环境状态的情况,我们称为完全可观测(Fully Observable),否则我们称为部分可观测(Partially Observable)环境;二是玩家的每个动作未必会产生立即反馈,某个动作可能在许多步之后才产生效果,强化学习模型允许这种延迟反馈的存在;三是这种反馈对人的学习过程而言未必是个数字,但是我们对强化学习智能体所得到的反馈进行数学抽象,将其转变为一个数字,称为奖励值。奖励值可以是状态的函数,也可以是状态和动作的函数,依具体问题而定。奖励值的存在是强化学习问题的一个基本假设,也是现有强化学习与监督式学习的一个主要区别
强化学习的决策过程通常由一个马尔可夫决策过程(Markov Decision Process,MDP)(马尔可夫决策过程即一个后续状态只依赖当前状态和动作而不依赖于历史状态的函数)描述,可以用一个数组\((\mathcal{S}, \mathcal{A}, R, \mathcal{T}, \gamma)\)来表示。\(\mathcal{S}\)和\(\mathcal{A}\)分别是状态空间和动作空间,\(R\)是奖励函数,\(R(s,a)\): \(\mathcal{S}\times \mathcal{A}\rightarrow \mathbb{R}\)为对于当前状态\(s\in\mathcal{S}\)和当前动作\(a\in\mathcal{A}\)的奖励值。从当前状态和动作到下一个状态的状态转移概率定义为\(\mathcal{T}(s^\prime|s,a)\): \(\mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow \mathbb{R}_+\)。\(\gamma\in(0,1)\)是奖励折扣因子(折扣因子可以乘到每个后续奖励值上,从而使无穷长序列有有限的奖励值之和)。强化学习的目标是最大化智能体的期望累计奖励值\(\mathbb{E}[\sum_t \gamma^t r_t]\)。
马尔可夫决策过程中的马尔可夫性质由以下定义
即当前状态转移只依赖于上一时刻状态,而不依赖于整个历史。这里的状态转移函数\(\mathcal{T}\)中省略了动作\(a\),马尔可夫性质是环境转移过程的属性,其独立于产生动作的决策过程。
基于马尔可夫性质,可以进一步推导出在某一时刻最优策略不依赖于整个决策历史,而只依赖于当前最新状态的结论。这一结论在强化学习算法设计中有着重要意义,它简化了最优策略的求解过程。
