11.2. 实现方法¶
下面讨论分布式训练系统实现的常用并行方法。首先给出并行方法的设计目标以及分类。然后详细描述各个并行方法。
11.2.1. 概述¶
分布式训练系统的设计目标是:将单节点训练系统转换成等价的并行训练系统,从而在不影响模型精度的条件下完成训练过程的加速。一个单节点训练系统往往如 图11.2.1所示。一个训练过程会由多个数据小批次(mini-batch)完成。在图中,一个数据小批次被标示为数据。训练系统会利用数据小批次生成梯度,提升模型精度。这个过程由一个训练程序实现。在实际中,这个程序往往实现了一个多层神经网络的执行过程。该神经网络的执行由一个计算图(Computational Graph)表示。这个图有多个相互连接的算子(Operator),每个算子会拥有计算参数。每个算子往往会实现一个神经网络层(Neural Network Layer),而参数则代表了这个层在训练中所更新的的权重(Weights)。
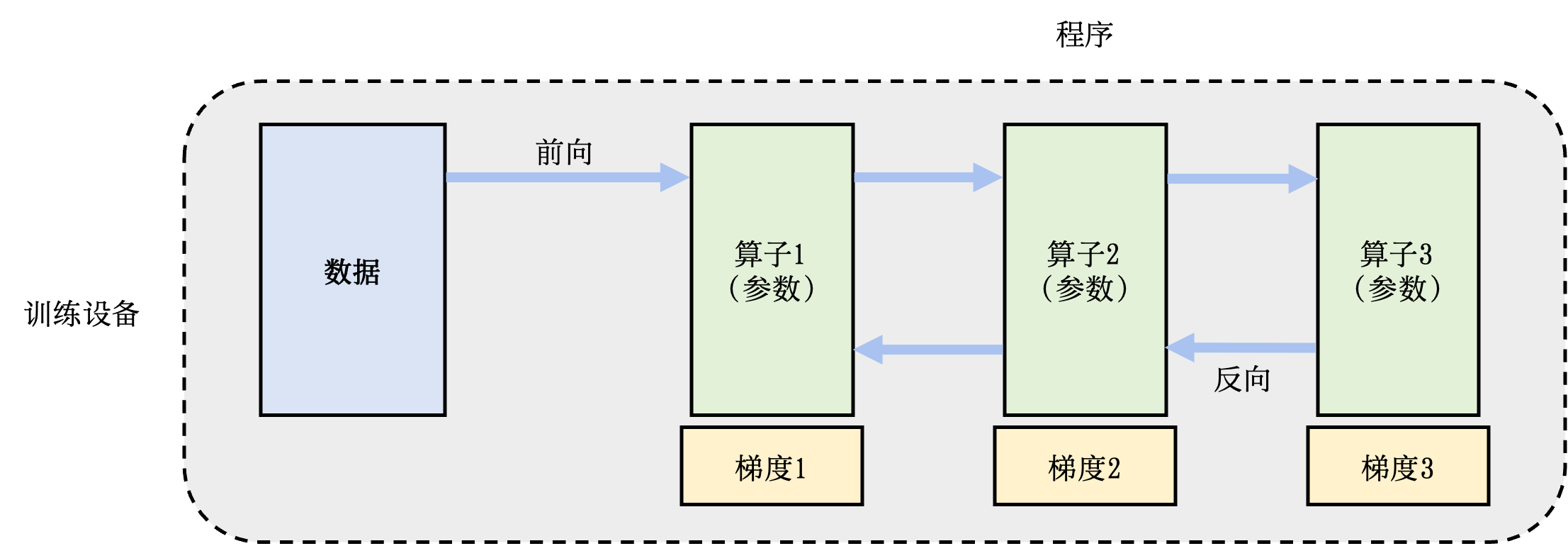
图11.2.1 单节点训练系统¶
为了更新参数,计算图的执行分为前向计算和反向计算两个阶段。前向计算的第一步会将数据读入第一个算子,该算子会根据当前的参数,计算出计算给下一个算子的数据。算子依次重复这个前向计算的过程(执行顺序:算子1,算子2,算子3),直到最后一个算子结束。最后的算子随之马上开始反向计算。反向计算中,每个算子依次计算出梯度(执行顺序:梯度3,梯度2,梯度1),并利用梯度更新本地的参数。反向计算最终在第一个算子结束。反向计算的结束也标志本次数据小批次的结束,系统随之读取下一个数据小批次,继续更新模型。
给定一个模型训练任务,人们会对数据和程序切分(Partition),从而完成并行加速。 表11.2.1总结了不同的切分方法。单节点训练系统可以被归类于单程序单数据模式。而假如用户希望使用更多的设备实现并行计算,首先可以选择对数据进行分区,并将同一个程序复制到多个设备上并行执行。这种方式是单程序多数据模式,常被称为数据并行(Data Parallelism)。另一种并行方式是对程序进行分区(模型中的算子会被分发给多个设备分别完成)。这种模式是多程序单数据模式,常被称为模型并行(Model Parallelism)。当训练超大型智能模型时,开发人员往往要同时对数据和程序进行切分,从而实现最高程度的并行。这种模式是多程序多数据模式,常被称为混合并行(Hybrid Parallelism)。
分类 |
单数据 |
多数据 |
|---|---|---|
单程序 |
单程序单数据:单点执行 |
单程序多数据:数据并行 |
多程序 |
多程序单数据:模型并行 |
多程序多数据:混合并行 |
接下来详细讲解各种并行方法的执行过程。
11.2.2. 数据并行¶
数据并行往往可以解决单节点算力不足的问题。这种并行方式在人工智能框架中最为常见,具体实现包括:TensorFlow DistributedStrategy、PyTorch Distributed、Horovod DistributedOptimizer等。在一个数据并行系统中,假设用户给定一个训练批大小为\(N\),并且希望使用\(M\)个并行设备来加速训练。那么,该训练批大小会被分为\(M\)个分区,每个设备会分配到\(N/M\)个训练样本。这些设备共享一个训练程序的副本,在不同数据分区上独立执行、计算梯度。不同的设备(假设设备编号为\(i\))会根据本地的训练样本计算出梯度\(G_i\)。为了确保训练程序参数的一致性,本地梯度\(G_i\)需要聚合,计算出平均梯度\((\sum_{i=1}^{N} G_i) / N\)。最终,训练程序利用平均梯度修正模型参数,完成小批次的训练。
图11.2.2展示了两个设备构成的数据并行训练系统(Data Parallel Training System)的例子。假设用户给定的数据批大小是64,那么每个设备会分配到32个训练样本,并且具有相同的神经网络参数(程序副本)。本地的训练样本会依次通过这个程序副本中的算子,完成前向计算和反向计算。在反向计算的过程中,程序副本会生成局部梯度。不同设备上对应的局部梯度(如设备1和设备2上各自的梯度1)会进行聚合,从而计算平均梯度。这个聚合的过程往往由集合通信的AllReduce操作完成。
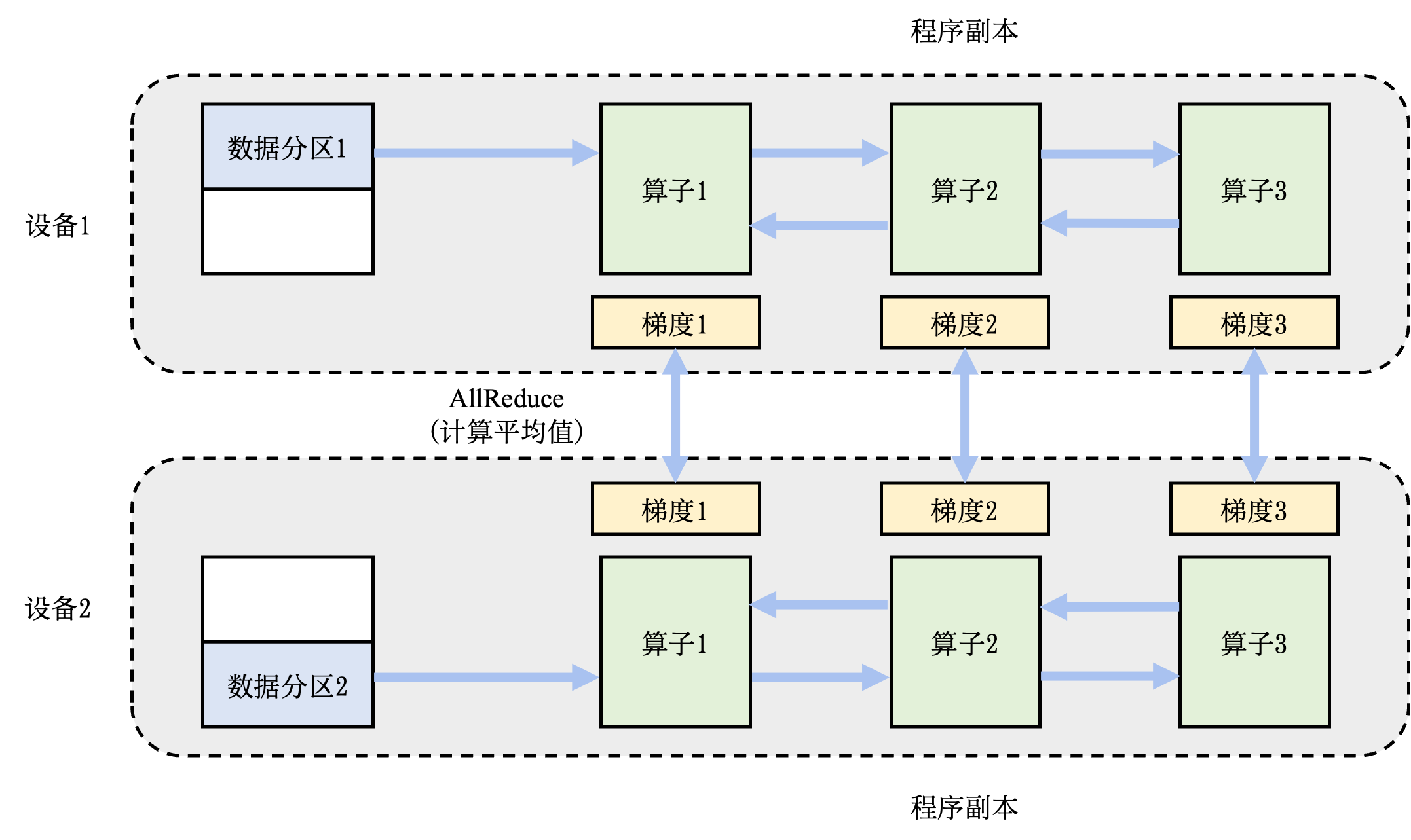
图11.2.2 数据并行训练系统¶
11.2.3. 模型并行¶
模型并行往往用于解决单节点内存不足的问题。一个常见的内存不足场景是模型中含有大型算子,例如深度神经网络中需要计算大量分类的全连接层。完成这种大型算子计算所需的内存可能超过单设备的内存容量。那么需要对这个大型算子进行切分。假设这个算子具有\(P\)个参数,而系统拥有\(N\)个设备,那么可以将\(P\)个参数平均分配给\(N\)个设备(每个设备分配\(P/N\)个参数),从而让每个设备负责更少的计算量,能够在内存容量的限制下完成前向计算和反向计算。这种切分方式是模型并行训练系统(Model Parallelism Training System)的一种应用,也被称为算子内并行(Intra-operator Parallelism)。
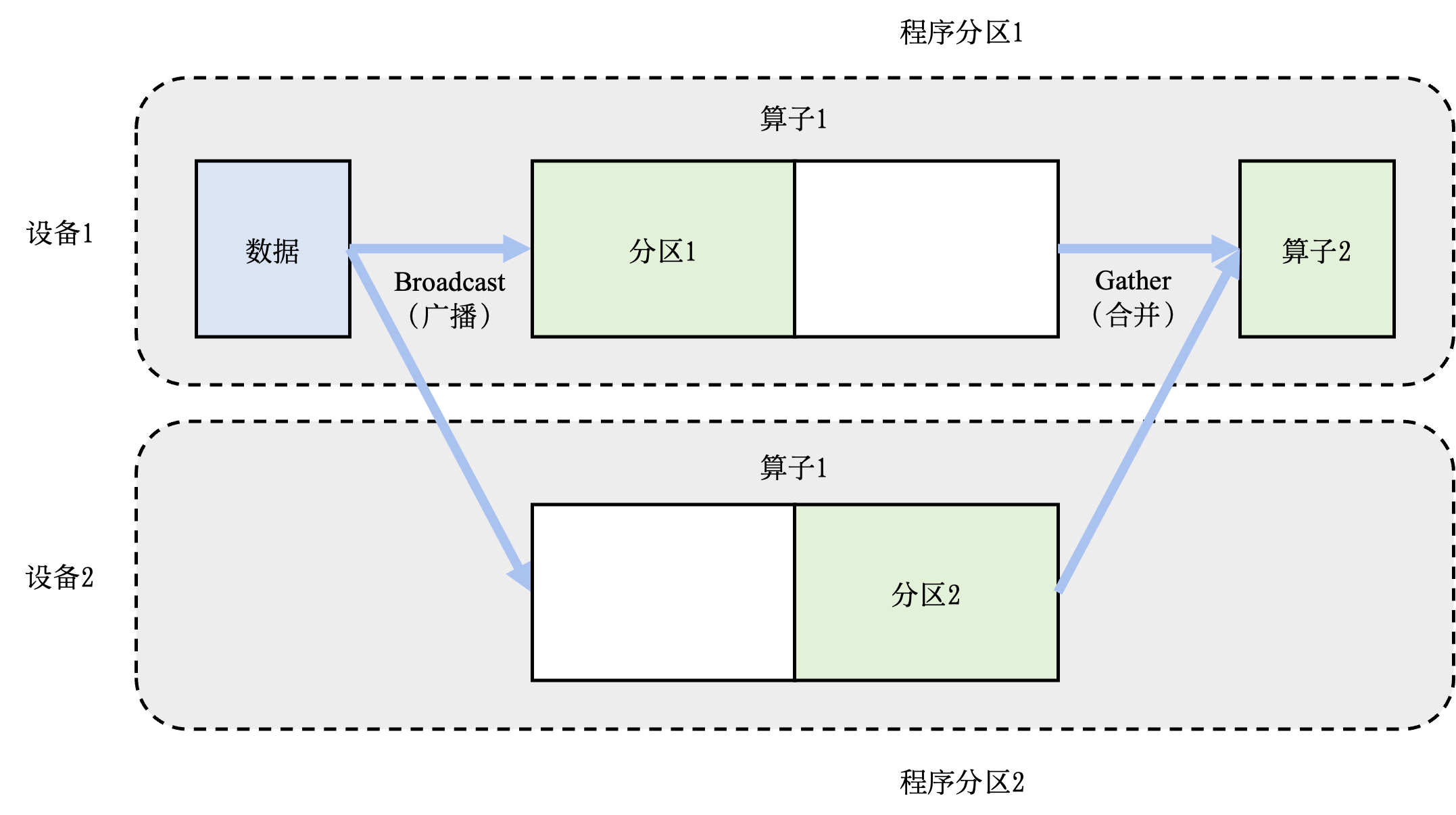
图11.2.3 模型并行训练系统:算子内并行¶
图11.2.3给出了一个由两个设备实现的算子内并行的例子。在这个例子中,假设一个神经网络具有两个算子,算子1的计算(包含正向和反向计算)需要预留16GB的内存,算子2的计算需要预留1GB的内存。而本例中的设备最多可以提供10GB的内存。为了完成这个神经网络的训练,需要对算子1实现并行。具体做法是,将算子1的参数平均分区,设备1和设备2各负责其中部分算子1的参数。由于设备1和设备2的参数不同,因此它们各自负责程序分区1和程序分区2。在训练这个神经网络的过程中,训练数据(按照一个小批次的数量)会首先传给算子1。由于算子1的参数分别由两个设备负责,因此数据会被广播(Broadcast)给这两个设备。不同设备根据本地的参数分区完成前向计算,生成的本地计算结果需要进一步合并,发送给下游的算子2。在反向计算中,算子2的数据会被广播给设备1和设备2,这些设备根据本地的算子1分区各自完成局部的反向计算。计算结果进一步合并计算回数据,最终完成反向计算。
另一种内存不足的场景是:模型的总内存需求超过了单设备的内存容量。在这种场景下,假设总共有\(N\)个算子和\(M\)个设备,可以将算子平摊给这\(M\)个设备,让每个设备仅需负责\(N/M\)个算子的前向和反向计算,降低设备的内存开销。这种并行方式是模型并行的另一种应用,被称为算子间并行(Inter-operator Parallelism)。
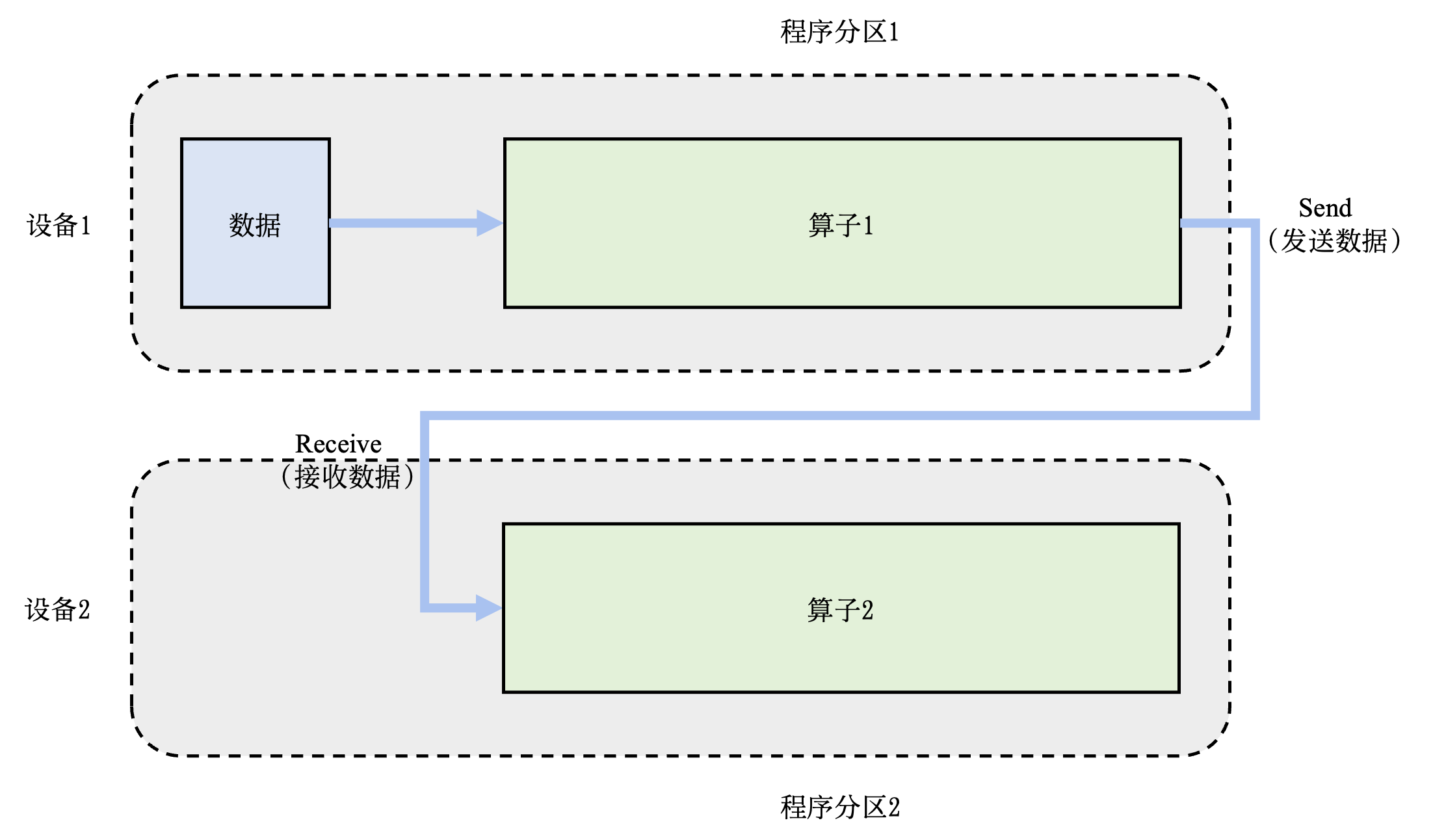
图11.2.4 模型并行训练系统:算子间并行¶
图11.2.4给出了一个由两个设备实现的算子间并行的例子。在这个例子中,假设一个神经网络具有两个算子,算子1和算子2各自需要10GB的内存完成计算,则模型总共需要20GB的内存。而每个设备仅能提供10GB内存。在这个例子中,用户可以把算子1放置在设备1上,算子2放置在设备2上。在前向计算中,算子1的输出会被发送(Send)给下游的设备2。设备2接收(Receive)来自上游的数据,完成算子2的前向计算。在反向计算中,设备2将算子2的反向计算结果发送给设备1。设备1完成算子1的反向计算,完成本次小批次(Mini-Batch)的训练。
11.2.4. 混合并行¶
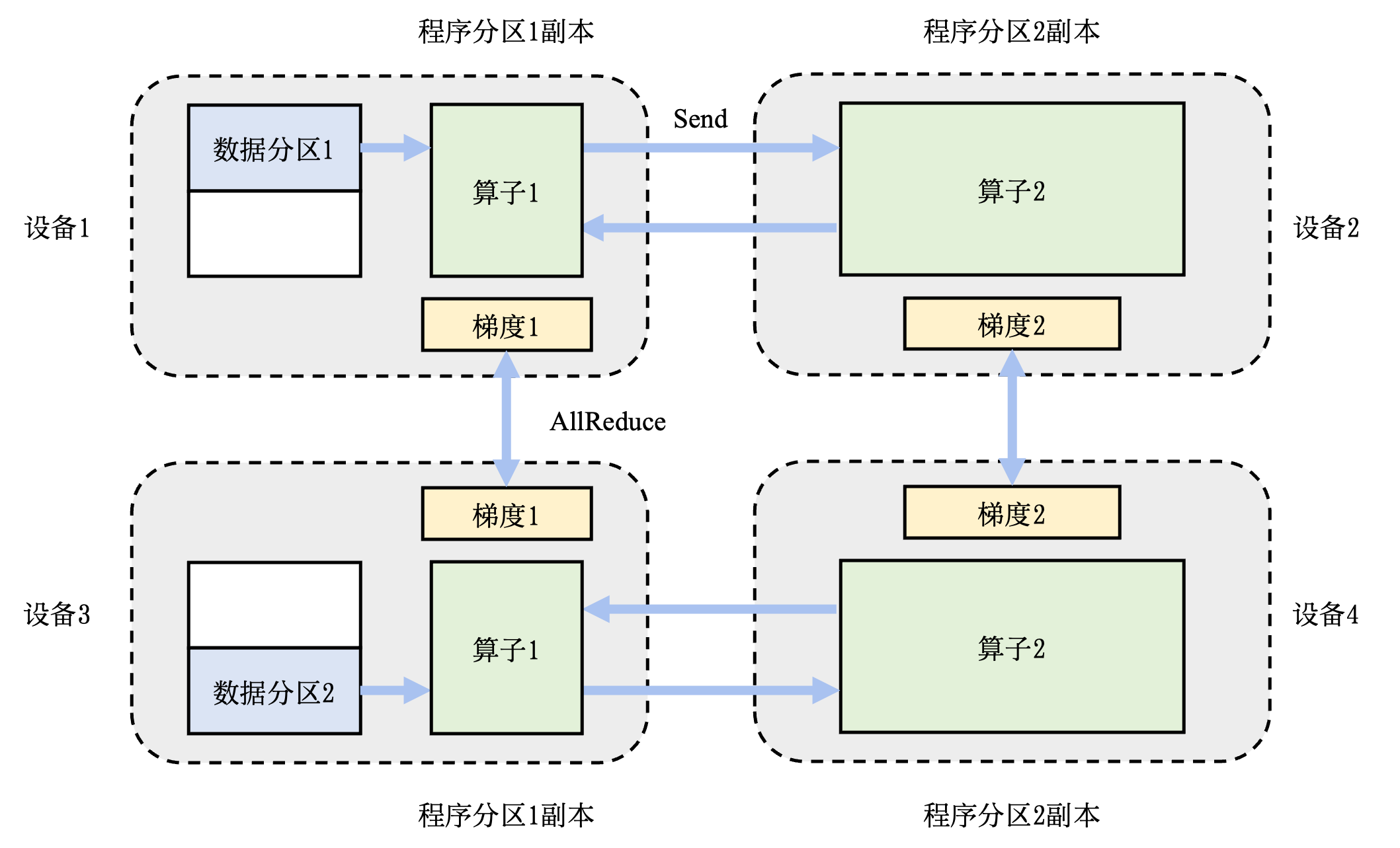
图11.2.5 混合并行系统¶
在训练大型人工智能模型中,往往会同时面对算力不足和内存不足的问题。因此,需要混合使用数据并行和模型并行,这种方法被称为混合并行。 图11.2.5提供了一个由4个设备实现的混合并行的例子。在这个例子中,首先实现算子间并行解决训练程序内存开销过大的问题:该训练程序的算子1和算子2被分摊到了设备1和设备2上。进一步,通过数据并行添加设备3和设备4,提升系统算力。为了达到这一点,对训练数据进行分区(数据分区1和数据分区2),并将模型(算子1和算子2)分别复制到设备3和设备4。在前向计算的过程中,设备1和设备3上的算子1副本同时开始,计算结果分别发送(Send)给设备2和设备4完成算子2副本的计算。在反向计算中,设备2和设备4同时开始计算梯度,本地梯度通过AllReduce操作进行平均。反向计算传递到设备1和设备3上的算子1副本结束。
11.3. 流水线并行¶
除了数据并行和模型并行以外,流水线并行是另一种常用的实现分布式训练的方法。流水线并行往往被应用在大型模型并行系统中。这种系统通过算子内并行和算子间并行解决单设备内存不足的问题。然而,这类系统的运行中,计算图中的下游设备(Downstream Device)需要长期持续处于空闲状态,等待上游设备(Upstream Device)的计算完成,才可以开始计算,这极大降低了设备的平均使用率。这种现象称为模型并行气泡(Model Parallelism Bubble)。
为了减少气泡,通常可以在训练系统中构建流水线。这种做法是将训练数据中的每一个小批次划分为多个微批次(Micro-Batch)。假设一个小批次有\(D\)个训练样本,将其划分为\(M\)个微批次,那么一个微批次就有\(D/M\)个数据样本。每个微批次依次进入训练系统,完成前向计算和反向计算,计算出梯度。每个微批次对应的梯度将会缓存,等到全部微批次完成,缓存的梯度会被加和,算出平均梯度(等同于整个小批次的梯度),完成模型参数的更新。
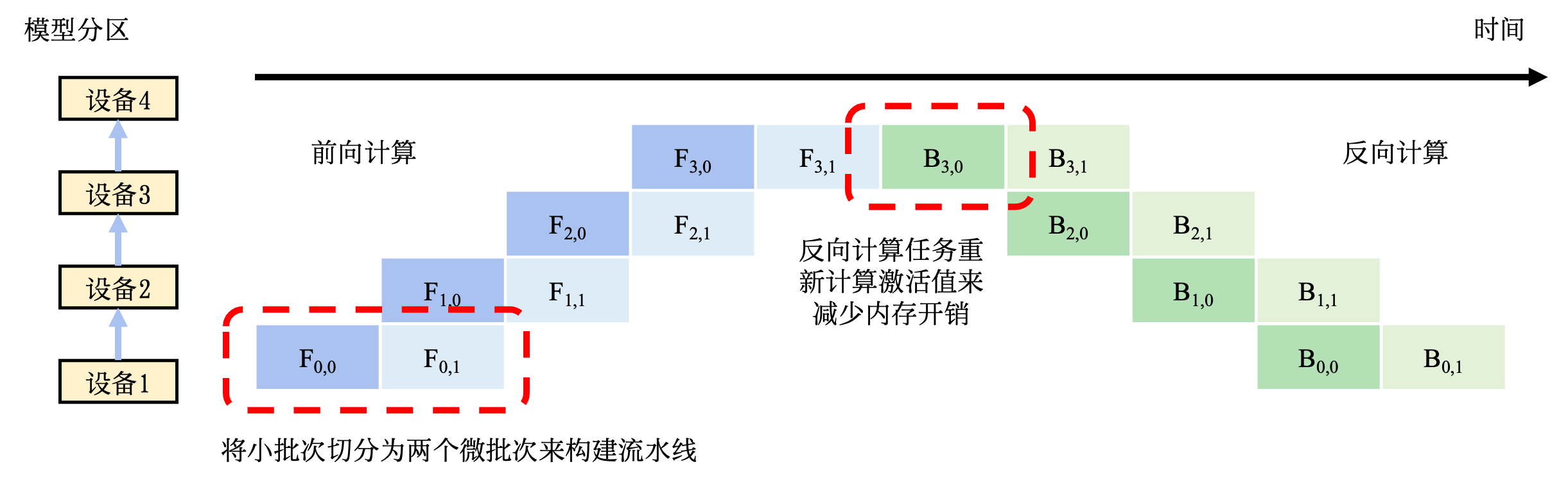
图11.3.1 流水线并行训练系统(Pipeline Parallel Training System)¶
图11.3.1 给出了一个流水线训练系统的执行例子。在本例中,模型参数需要切分给4个设备存储。为了充分利用这4个设备,将小批次切分为两个微批次。假设\(F_{i,j}\)表示第\(j\)个微批次的第\(i\)个前向计算任务,\(B_{i,j}\)表示第\(j\)个微批次的第\(i\)个反向计算任务。当设备1完成第一个微批次的前向计算后(表示为\(F_{0,0}\)),会将中间结果发送给设备2,触发相应的前向计算任务(表示为\(F_{1,0}\))。与此同时,设备1也可以开始第二个微批次的前向计算任务(表示为\(F_{0,1}\))。前向计算会在流水线的最后一个设备,即设备3,完成。
系统于是开始反向计算。设备4开始第1个微批次的反向计算任务(表示为\(B_{3,0}\))。该任务完成后的中间结果会被发送给设备3,触发相应的反向计算任务(表示为\(B_{2,0}\))。与此同时,设备4会缓存对应第1个微批次的梯度,接下来开始第2个微批次计算(表示为\(B_{3,1}\))。当设备4完成了全部的反向计算后,会将本地缓存的梯度进行相加,并且除以微批次数量,计算出平均梯度,该梯度用于更新模型参数。
需要注意的是,计算梯度往往需要前向计算中产生的激活值。经典模型并行系统中会将激活值缓存在内存中,反向计算时就可以直接使用,避免重复计算。而在流水线训练系统中,由于内存资源紧张,前向计算中的激活值往往不会缓存,而是在反向计算中重新计算(Recomputation)。
在使用流水线训练系统中,时常需要调试微批次的大小,从而达到最优的系统性能。当设备完成前向计算后,必须等到全部反向计算开始,在此期间设备会处于空闲状态。在 图11.3.1中,可以看到设备1在完成两个前向计算任务后,要等很长时间才能开始两个反向计算任务。这其中的等待时间即被称为流水线气泡(Pipeline Bubble)。为了减少设备的等待时间,一种常见的做法是尽可能地增加微批次的数量,从而让反向计算尽可能早开始。然而,使用非常小的微批次,可能会造成微批次中的训练样本不足,从而无法充分的利用起来硬件加速器中的海量计算核心。因此最优的微批次数量由多种因素(如流水线深度、微批次大小和加速器计算核心数量等)共同决定。
