7.4. Performance Optimization Methods¶
Hardware accelerators boast intricate computational and memory architectures. To maximize their performance, developers frequently need to grasp a variety of performance optimization methods. Common methods encompass enhancing arithmetic intensity, capitalizing effectively on shared memory, optimizing the memory load/store pipeline, among others. The subsequent sections will elucidate these methods through practical programming examples, all aimed towards a singular objective: accelerating an FP32 GEMM program.
7.4.1. Implementing General Matrix Multiplication¶
Code lst:cpu shows a reference implementation of GEMM in C++.
lst:cpu
float A[M][K];
float B[K][N];
float C[M][N];
float alpha, beta;
for (unsigned m = 0; m < M; ++m) {
for (unsigned n = 0; n < N; ++n) {
float c = 0;
for (unsigned k = 0; k < K; ++k) {
c += A[m][k] * B[k][n];
}
C[m][n] = alpha * c + beta * C[m][n];
}
}
ach element in matrix \(C\) is independently computed, and numerous
GPU threads can be launched to compute the corresponding elements in
matrix \(C\) in parallel. The GPU kernel function is shown in
Code lst:gpu.
lst:gpu
__global__ void gemmKernel(const float * A,
const float * B, float * C,
float alpha, float beta, unsigned M, unsigned N,
unsigned K) {
unsigned int m = threadIdx.x + blockDim.x * blockIdx.x;
unsigned int n = threadIdx.y + blockDim.y * blockIdx.y;
if (m >= M || n >= N)
return;
float c = 0;
for (unsigned k = 0; k < K; ++k) {
c += A[m * K + k] * B[k * N + n];
}
c = c * alpha;
float result = c;
if (beta != 0) {
result = result + C[m * N + n] * beta;
}
C[m * N + n] = result;
}
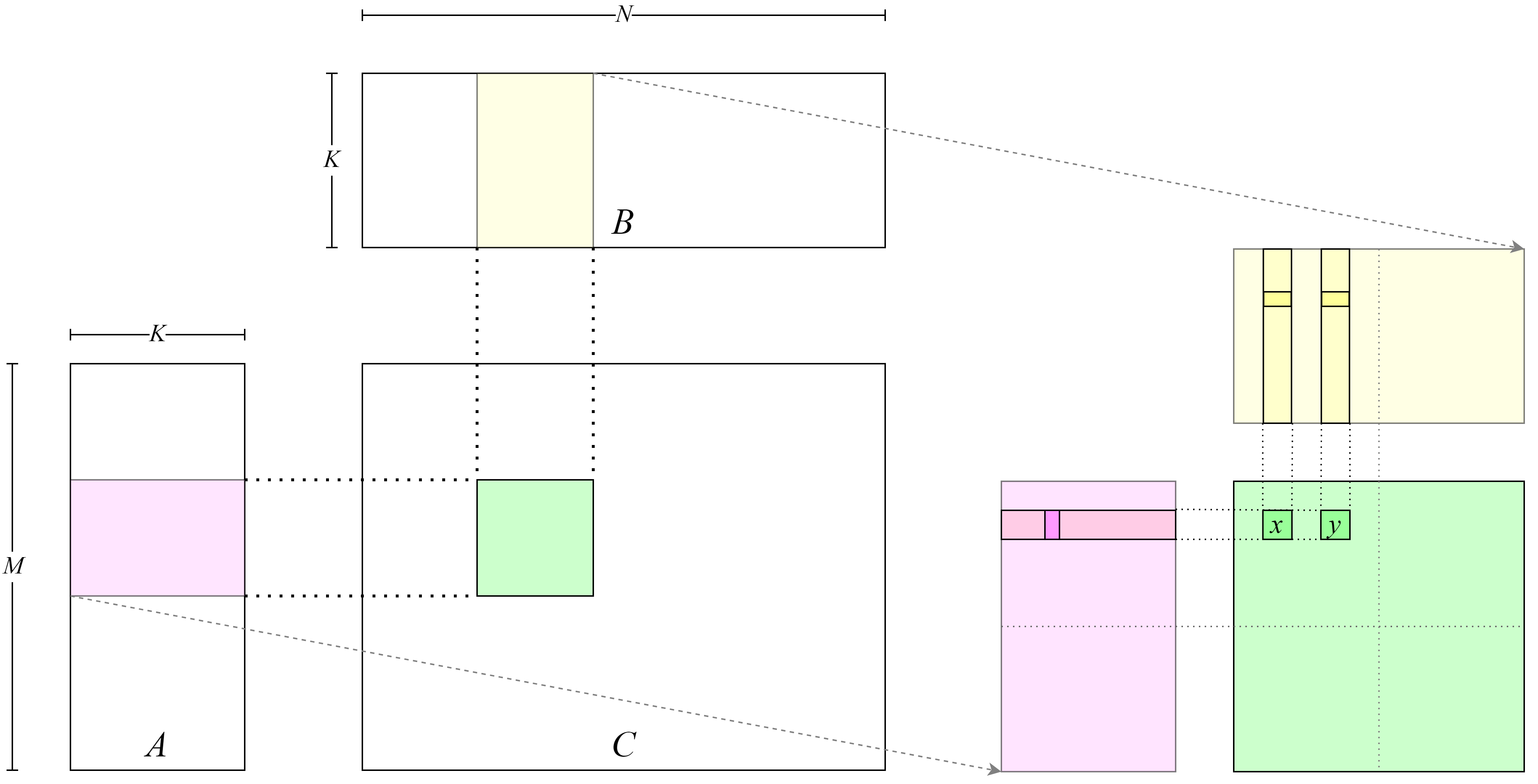
Figure :numref:cuda_naive_gemm shows the layout of the
implementation. Each element in matrix \(C\) is computed by one
thread. The row index \(m\) and column index \(n\) of the
element in matrix \(C\) corresponding to the thread are computed in
lines 5 and 6 of the GPU kernel. Then, in lines 9 to 11, the thread
loads the row vector in matrix \(A\) according to the row index and
the column vector in matrix \(B\) according to the column index,
computes the vector inner product. The thread also stores the result
back to \(C\) matrix in line 17.
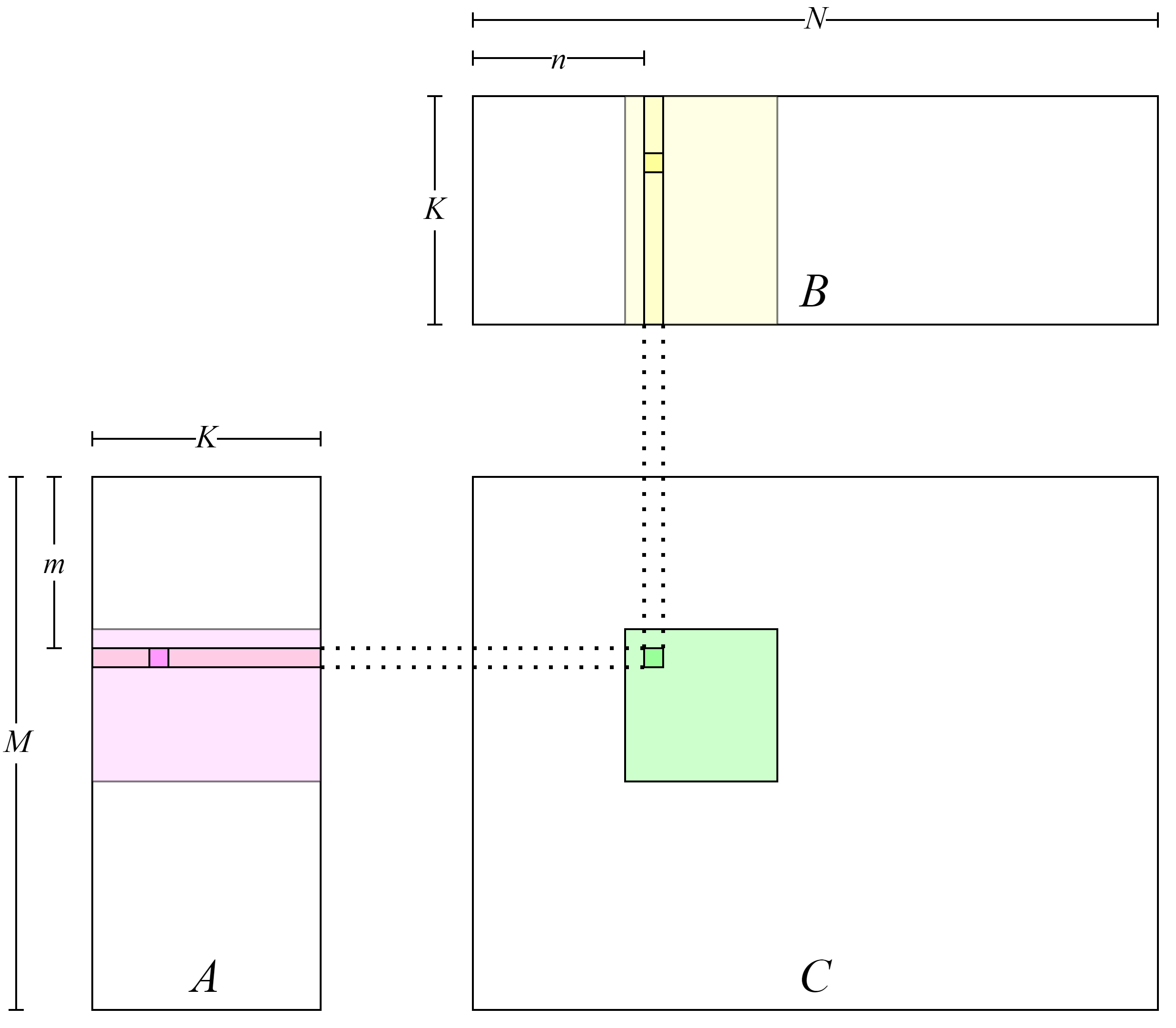
Fig. 7.4.1 Simple implementation ofGEMM¶
The method of launching the kernel function is shown in
Code lst:launch.
lst:launch
void gemmNaive(const float *A, const float *B, float *C,
float alpha, float beta, unsigned M,
unsigned N, unsigned K) {
dim3 block(16, 16);
dim3 grid((M - 1) / block.x + 1, (N - 1) / block.y + 1);
gemmKernel<<<grid, block>>>(A, B, C, alpha, beta, M, N, K);
}
Each thread block processes \(16\times16\) elements in matrix \(C\). Therefore, \((M - 1) / 16 + 1 \times (N - 1) / 16 + 1\) thread blocks are used to compute the entire matrix \(C\).
Eigen is used to generate data and compute the GEMM result on the CPU. In addition, error computing and time profiling code are implemented for the GPU computing result. For details, see first_attempt.cu. After the program is compiled and executed, output results are as follows:
Average time: 48.961 ms
Max error: 0.000092
The peak GPU throughput can be approximated by using the following formula: 2 \(\times\) Frequency \(\times\) Number of single-precision compute units. The number of single-precision compute units equals the number of SMs in the GPU multiplied by the number of single-precision compute units in each SM. The results are as follows:
FP32 peak throughput 29767.680 GFLOPS
Average Throughput: 185.313 GFLOPS
A significant gap exists between the performance that can be achieved by the current code and the peak device performance. In an entire computing process, the process with the highest computing density is matrix multiplication \(A\times B\). Its time complexity is \(O(M*N*K)\), whereas that time complexity of the entire computing process is \(O(M*N*K+2*M*N)\). Therefore, optimizing matrix multiplication is key to improving performance.
7.4.2. Enhancing Arithmetic Intensity¶
Arithmetic intensity is the ratio of computational instructions to load/store instructions. Modern GPUs typically have numerous compute units, constrained only by a limited load/store bandwidth. This limitation often leaves these units waiting for data loading in a program. Thus, boosting arithmetic intensity is a crucial step to improve program performance.
In the GPU kernel function discussed previously, we can approximate its arithmetic intensity by dividing the total number of floating-point operations by the number of data reads. When calculating the inner product within \(K\) loops, floating-point multiplication and addition operations occur each time elements from matrix \(A\) and \(B\) are loaded. Consequently, the arithmetic intensity is 1, derived from two 32-bit floating-point operations divided by two 32-bit data load/store instructions.
In the original code, each thread handles one element in matrix \(C\), computing the inner product of a row in matrix \(A\) and a column in matrix \(B\). In essence, we can elevate the arithmetic intensity by amplifying the elements in matrix \(C\) that each thread can process, computing the inner product of multiple rows in matrix \(A\) and multiple columns in matrix \(B\). More specifically, if \(m\) elements in matrix \(A\) and \(n\) elements in matrix \(B\) are loaded concurrently while calculating the inner product in \(K\) loops, there are \(m+n\) 32-bit load/store instructions and \(2mn\) 32-bit computational instructions. Hence, the arithmetic intensity becomes \(\frac{2mn}{m+n}\). Therefore, by increasing \(m\) and \(n\), we can optimize the arithmetic intensity.
In the preceding section, a float pointer was employed to access
global memory and store data in it, utilizing the hardware instructions
LDG.E and STG.E. Multiple float elements can be loaded
concurrently using the 128-bit wide instructions LDG.E.128 and
STG.E.128. These wide instructions can streamline the instruction
sequence, potentially saving dozens of instruction issue cycles compared
to four standard instructions, thereby enabling the issue of more
computational instructions within the saved time. Wide instructions can
also enhance the cache line hit rate. Despite these benefits, we advise
against the blanket use of wide instructions in all code. Instead,
programmers should prioritize direct optimization methods, such as
parallel design and local data reuse.
A specific implementation is stacking four float numbers to form a
128-bit float4 class. The load/store operations will be completed
using a wide instruction for the float4 class. For details about the
code implementation, see
util.cuh.
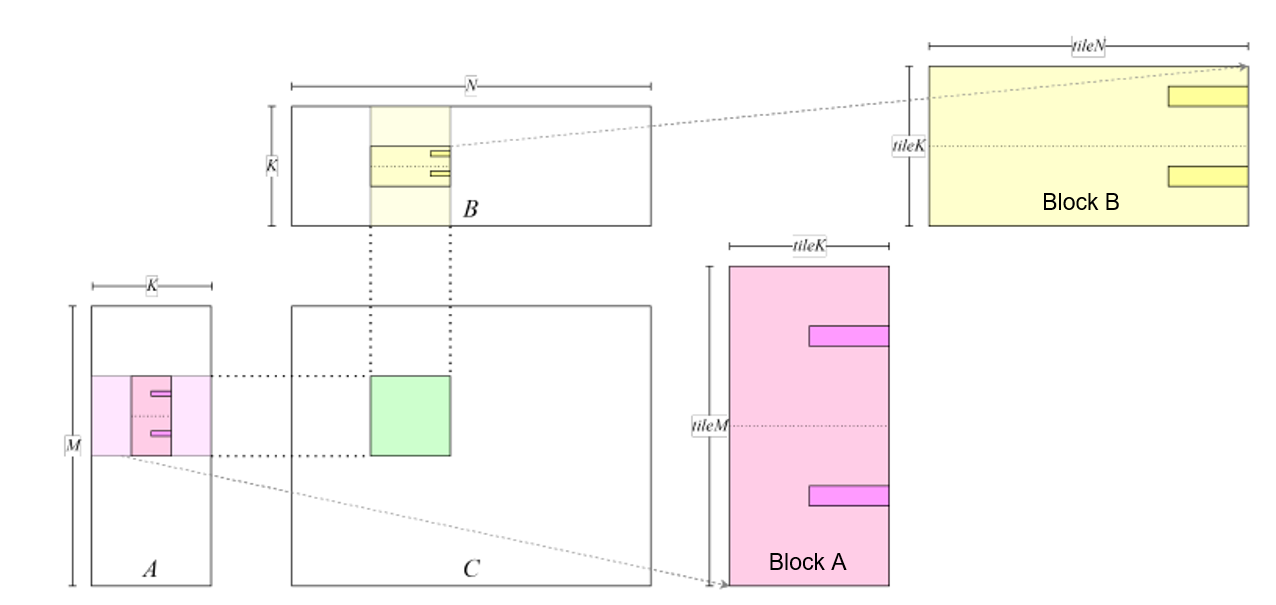
Note that each thread needs to load four float numbers (instead of
one) from matrix \(A\) and matrix \(B\), requiring each thread
to process \(4\times 4\) blocks (thread tile) in matrix
\(C\). Each thread loads data from matrix \(A\) and matrix
\(B\) from left to right and from top to bottom, computes the data,
and stores the data to matrix \(C\), as shown in
Figure :numref:use_float4.
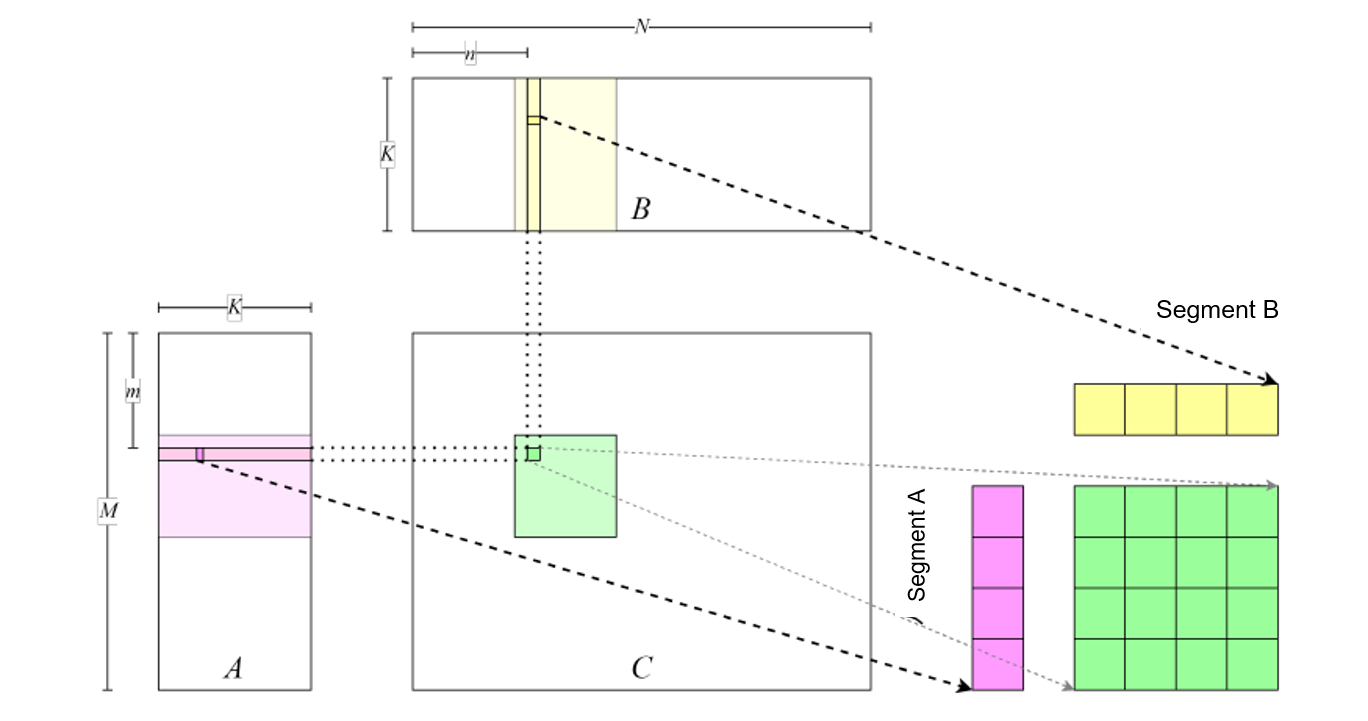
Fig. 7.4.2 Enhancing arithmeticintensity¶
For details about the complete code, see
gemm_use_128.cu.
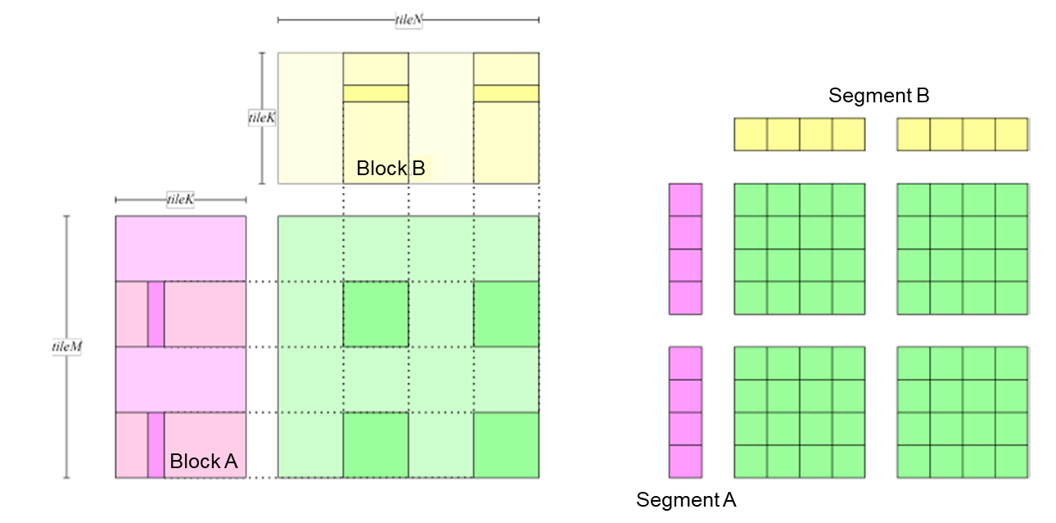
We can further increase the amount of data processed by each thread in
order to improve the arithmetic intensity more, as shown in
Figure :numref:use_tile. For details about the code used to
achieve this, see
gemm_use_tile.cu.
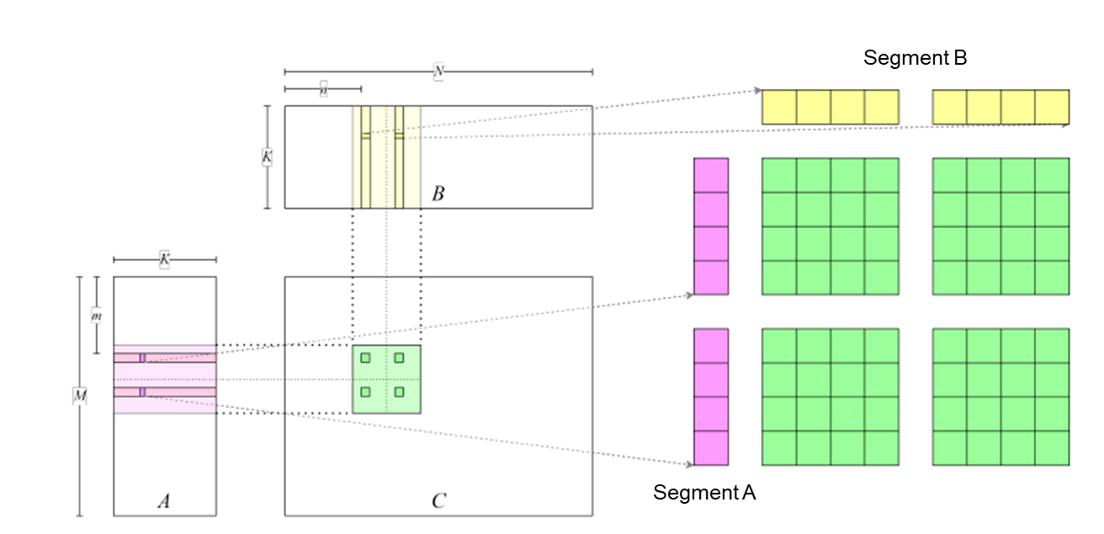
Fig. 7.4.3 Further enhancement of the arithmetic intensity by adding matrixblocks processed by eachthread¶
The test results are as follows:
Max Error: 0.000092
Average Time: 6.232 ms, Average Throughput: 1378.317 GFLOPS
To sample and analyze performance indicators, we will use the analysis tool Nsight Compute released by NVIDIA. This tool, designed for GPU kernel functions, samples and collects GPU activity data by hooking drivers. The following commands can be used to analyze the performance:
bash
ncu --set full -o <profile_output_file> <profile_process>
–set full indicates that all data is sampled. -o indicates that
the result is output as a file. <profile_output_file> indicates the
output file name without the file name extension. <profile_process>
indicates the executable file to be analyzed and its arguments. For
example, to analyze first_attempt and name the output result
first_attepmt_prof_result, run the following instructions:
ncu --set full -o first_attepmt_prof_result ./first_attempt
If the system displays a message indicating that you do not have
permission to run this command, prefix it with sudo and run it
again. After obtaining the output file, the program nv-nsight-cu can
be used to view the file. We compared the profiling results of the new
GPU kernel function and the previous one.
The result shows that the number of LDG instructions decreases by
84%, and the value of Stall LG Throttle decreases by 33%. By using
wide instructions to increase the compute density, we are able to reduce
the number of global load/store instructions, thereby cutting the amount
of time needed to wait before issuing instructions. The improvement on
Arithmetic Intensity proves that our analysis of the arithmetic
intensity is correct. The gemm_use_tile.cu test results are as follows:
Max Error: 0.000092
Average Time: 3.188 ms, Average Throughput: 2694.440 GFLOPS
The analysis using Nsight Compute shows that the code can also improve
other indicators, such as Stall LG Throttle.
7.4.4. Reducing Register Usage¶
In previous sections, the data blocks that store matrix \(A\) in the shared memory are arranged in a row-first manner, and the shared memory is loaded by row. We can instead adopt a column-first manner in order to reduce loops and loop variables, thereby reducing the number of registers and improving performance.
For details about the complete code, see gemm_transpose_smem.cu.
The test results are as follows:
Max Error: 0.000092
Average Time: 0.610 ms, Average Throughput: 14083.116 GFLOPS
Analysis by Nsight Compute shows that Occupancy increases by 1.3%.
This is because only 111 registers are used (17 fewer than used by the
previous GPU kernel function). The benefit of reducing the number of
registers varies depending on the GPU architecture. Observations have
shown that the number of STS instructions increases and bank
conflicts occur, meaning that using fewer registers may not have a
positive impact on other GPU architectures.
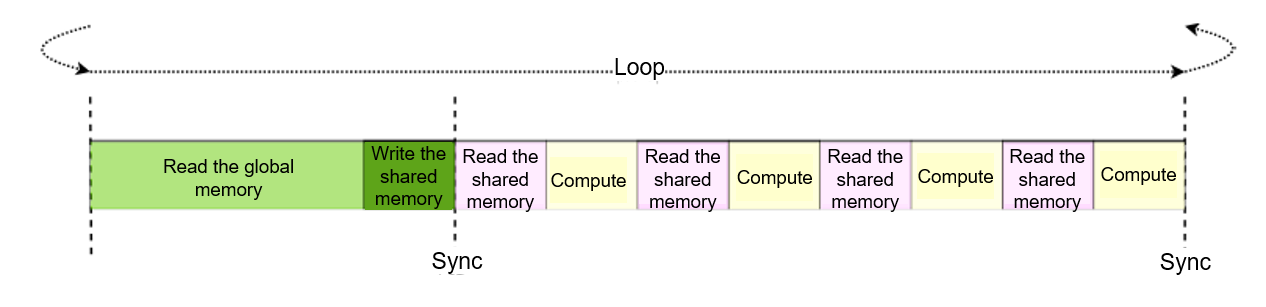
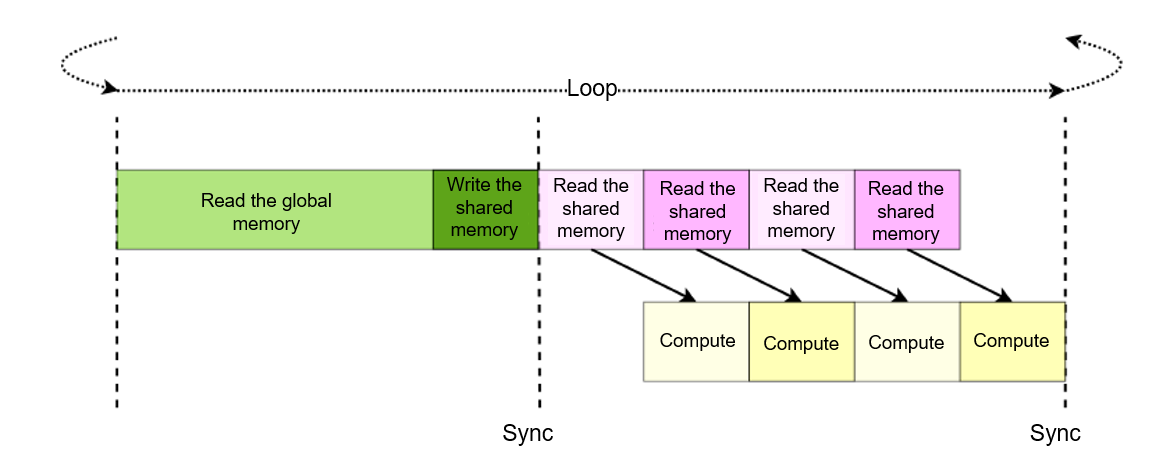
7.4.6. Hiding Global Memory Loading Latency¶
To load data from the global memory, a GPU uses the textttLDG
instruction, the behavior of which is similar to the LDS instruction
used to load data from the shared memory as discussed in the previous
section. At the beginning of each of the \(\frac{K}{tileK}\) outer
loops, instructions that load the data tiles in matrix \(A\) for the
next loop are issued. Because this data is not required by any inner
loop in a given outer loop, the computational processes in the inner
loop will not wait for the read instruction to be completed, thereby
hiding the global memory loading latency. We can also enable data in
buffer to be written to tile in the last loop in the inner loop
after \(tileK - 1\) loops are executed, further reducing the latency
of writing data to tile. Figure :numref:hide_global_latency
shows the optimized pipeline.
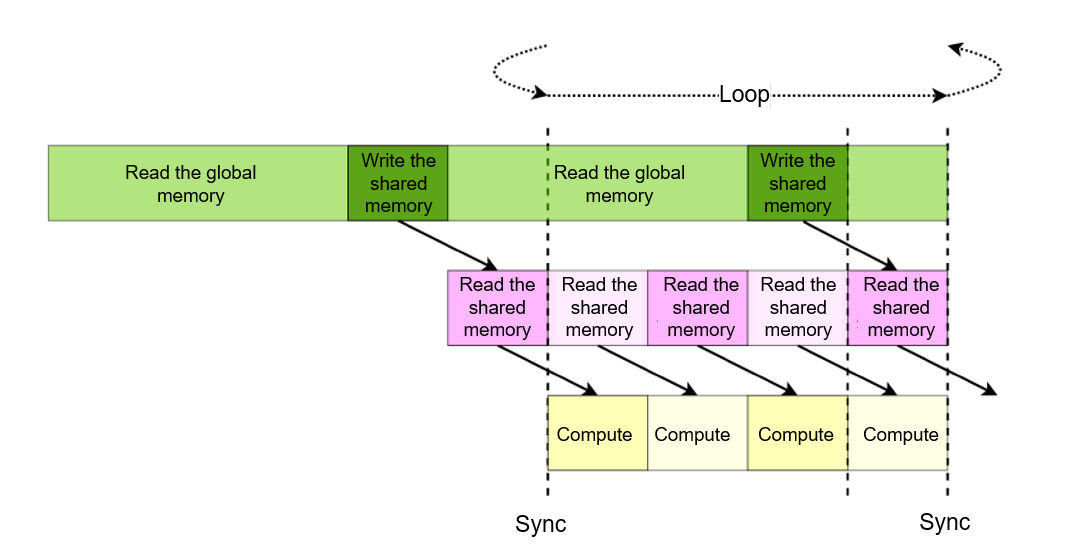
Fig. 7.4.9 Pipeline that hides the global memory loadinglatency¶
For details about the complete code, see gemm_final.cu.
The test results are as follows:
Max Error: 0.000092
Average Time: 0.542 ms, Average Throughput: 15838.302 GFLOPS
Similar to the Stall Short Scoreboard results obtained in the
previous section, analysis by Nsight Compute shows that the value of
Stall Long Scoreboard (a global memory indicator) decreases by 67%.
Such a significant decrease demonstrates that prefetching data can hide
the global memory to reduce the loading latency.
7.4.7. Performance Optimization Principles¶
So far, we have discussed various methods to enhance the performance of an accelerator. Even though other methods exist, the principles of performance optimization generally adhere to the following:
Increasing parallelism through resource mapping: Multi-level parallel resources (
blocks,warps, andthreads) are mapped to the data needing computation and transfer to enhance program parallelism.Reducing memory access latency through memory structure optimization: Based on the recognition of data reuse within the same
blockduring computation, the reused data is stored in local memory (like shared memory and registers) to increase locality.Reducing the instruction issue overhead through optimizing instruction execution: The
#pragma unrollfunction is used to unroll loops in order to improve the degree of parallelism at the instruction level and reduce logic judgment. The vectorized load instruction is used to increase bandwidth. For the Ampere architecture, the maximum vectorized load instruction isLDG.E.128, and the data type for data loading isfloat4.Hiding load/store latency by optimizing the memory access pipeline: In instances where the in-memory data undergoes modifications (such as the movement of matrix data), we can optimize the memory access pipeline. This way, the accelerator performs computations during the intervals between data movement, thereby concealing the latency associated with data movement.