12.6. Multi-agent Reinforcement Learning System ¶
The preceding examples help explain the role of reinforcement learning
in multi-agent problems. At present, cutting-edge multi-agent
reinforcement learning algorithms are capable of solving large-scale
complex multi-agent problems. For example, in games like StarCraft II
and Dota 2, AlphaStar (an agent developed by DeepMind) and OpenAI Five
(an agent developed by OpenAI) already surpass the top human players.
Chinese companies such as Tencent and Inspir.ai have also proposed their
multi-agent reinforcement learning solutions TStarBot-X and StarCraft
Commander (SCC) for StarCraft II. For such a highly complex gaming
environment, the entire training process — which may be divided into
multiple phases — raises extremely high requirements on distributed
computing systems. Take AlphaStar as an example. It combines supervised
learning and reinforcement learning in agent training. In order to
quickly gain good capabilities during the early stage of training,
supervised learning often resorts to using a large amount of annotated
data provided by professional human players. Once this is achieved, the
training then switches to the reinforcement learning process, and the
fictitious self-play algorithm mentioned earlier comes into play (i.e.,
self-game). To obtain the best-performing agent among the numerous
candidates, the algorithm needs to explore the entire strategy space. In
this way, instead of training one individual strategy, it trains a
league (i.e., strategy cluster). And by filtering the league in a manner
similar to evolutionary algorithms, it finds the best-performing
strategy. As shown in Figure :numref:
ch011/ch11-marl-train
, each
agent needs to play games with exploiters and other agents. An
exploiter
represents the best response strategy confronting a specific
agent strategy — such confrontation helps improve the anti-exploitation
capability of the agent strategy. The act of training and filtering
numerous agent strategies is called
league training
(or
population-based training
), which aims to improve strategy population
diversity through distributed training in order to attain higher model
performance. In practice, this type of method relies on a distributed
system to implement multi-agent training and gaming, reflecting the
dependency of multi-agent reinforcement learning on distributed
computing.
Now, let’s look at the difficulties involved in building a multi-agent reinforcement learning system in the following sections.
12.6.1. Curse of Multi-agent ¶
This difficulty refers to the complexity caused by multiple agents. The most direct change from a single-agent system to a multi-agent one is that the number of agents changes from 1 to more than 1. For an \(N\) -agent system where each agent is independent of others, this change will lead to an exponential increase in the complexity of the strategy representation space, that is, \(\tilde{O}(e^N)\) . Take a single-agent system with a discrete strategy space as an example. If the size of the state space is \(S\) , that of the action space is \(A\) , and the game step is \(H\) , then the size of the discrete strategy space is \(O(HSA)\) . If we extend the game to an \(N\) -player game, the joint distribution space of all player strategies in the most general case — all players have a symmetric action space (size is \(A\) ) and do not share any structure information — will be \(O(HSA^N)\) in size. This is because the strategy space of each independent player is multiplied to form this joint space, specifically, \(\mathcal{A}=\mathcal{A}_1\times\dots\mathcal{A}_N\) . As a direct consequence, the algorithm search complexity increases.
To address this issue, the original single-agent system needs to be extended to a multi-agent system for strategy optimization. This means that each parallel module in the single-agent distributed system needs to be extended for each agent in the multi-agent system. In complex cases, there are still many other factors to take into account, for example, communications and heterogeneity between agents — sometimes different agents are represented by models that are not completely symmetrical and may use different algorithms for optimization.
12.6.2. Complex Game Types ¶
From the perspective of game theory, multi-agent systems are associated with complex game types, for example, games can be directly classified as competitive, cooperative, or mixed. In competitive games, the most typical one is a two-player zero-sum game, such as the rock-paper-scissors game discussed in the previous section. In such games, the Nash equilibrium strategy is generally a mixed strategy. That is, equilibrium cannot be achieved through a single pure strategy; however, pure-strategy Nash equilibrium does exist in a few zero-sum games. In cooperative games, multiple agents need to cooperate in order to improve the overall reward. Related research typically adopts the value decomposition approach to assign the rewards obtained by all agents to individual agents. Typical algorithms include value-decomposition network (VDN) , counterfactual multi-agent (COMA) , and QMIX .
In mixed games, some agents may cooperate with each other while others or sets of agents compete with each other. Usually non-zero-sum and non-pure-cooperative games are mixed games. An example is the prisoner’s dilemma (see Table Table 12.6.1 for its reward values), in which two prisoners (players) each have two actions, silence and betrayal. The absolute value of the reward is the number of years that each prisoner will be sentenced to. Because the sum of the reward values is not a constant, prisoner’s dilemma is a non-zero-sum game. And given that one prisoner may choose silence while the other chooses betrayal (in that case, the former gets a reward of –3 and the latter gets 0), it cannot be considered a pure competitive or pure cooperative game. In a cooperation strategy, both prisoners choose silence and each gets a reward of –1. Although this strategy seems better than others, it is not the game’s Nash equilibrium strategy, which assumes that all player strategies are separate and cannot form a joint distribution, prohibiting information communication and potential cooperation between players. As such, the Nash equilibrium strategy of the prisoner’s dilemma is that both players choose to betray.
In consideration of such games, single-agent reinforcement learning cannot be directly used to optimize the strategy of each agent in a multi-agent system. Single-agent reinforcement learning is generally a process of finding an extremum, whereas solving the Nash equilibrium strategy of a multi-agent system is to find the maximum-minimum (i.e., saddle points). The two types of systems also differ from an optimization perspective. Complex relationships need to be represented by a more generalized system — this poses another challenge to the construction of a multi-agent system. There are also other types of games in multi-agent systems, including single-round or multi-round games, simultaneous decision or sequential decision, etc. Each type corresponds to different algorithms, but the existing multi-agent systems are targeted at a specific game type or algorithm. We are in urgent need of generalized multi-agent reinforcement learning systems, especially distributed systems.
|
|
Silence |
Betrayal |
|---|---|---|
|
Silence |
(–1, –1) |
(–3, 0) |
|
Betrayal |
(0, –3) |
(–2, –2) |
12.6.3. Algorithm Heterogeneity ¶
From the simple multi-agent algorithms described earlier, such as self-play and fictitious self-play, we can conclude that multi-agent algorithms sometimes involve multiple rounds of the single-agent reinforcement learning process and that algorithms vary according to game types. For cooperative games, many algorithms are based on the idea of credit assignment. Central to these algorithms is the ability to properly assign the rewards obtained by multiple agents to individual agents. According to the execution mode employed, such algorithms fall into three categories: centralized training centralized execution, centralized training decentralized execution, and decentralized training decentralized execution. These categories describe the uniformity of different agents’ training and execution processes. For competitive games, various approximation methods (including fictitious self-play , double oracle , and mirror descent ) are used to compute the Nash equilibrium. A single agent’s attempt to obtain a single optimal strategy through reinforcement learning is regarded as an action , and the Nash equilibrium needs to be approximated on the meta-problem composed of these actions. Due to the significant differences between how existing algorithms handle similar problems, building a unified multi-agent reinforcement learning system is difficult.
12.6.4. Hybrid Methods ¶
In work such as AlphaStar , reinforcement learning algorithms alone cannot obtain a good strategy in a multi-agent system; instead, we need to employ other learning methods, such as imitation learning. For example, we can create labeled training samples from the gaming records of top human players in order to pre-train agents. Due to the complexity of these large-scale games, such a method allows us to quickly improve the performance of agents in the early stage of training. In terms of the learning system as a whole, a combination of different learning paradigms is required, for example, reasonably switching between imitation learning and reinforcement learning. This means that we cannot consider the large-scale multi-agent system as solely a reinforcement learning system; instead, it is one that requires cooperation between many other learning and coordination mechanisms.
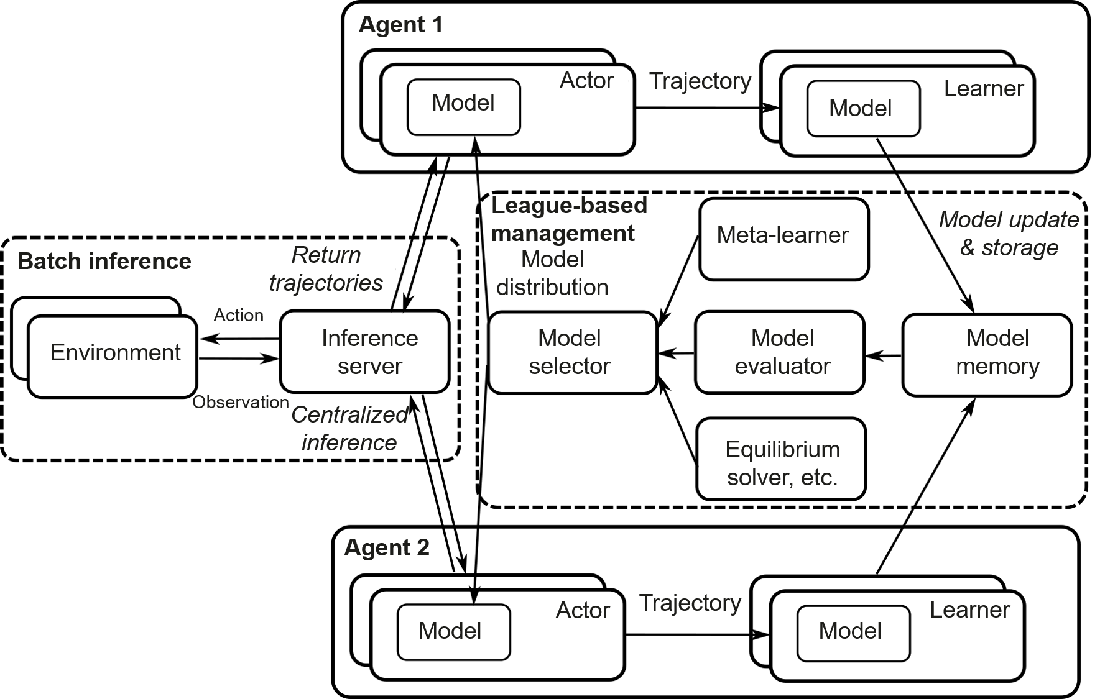
Figure Fig. 12.6.2 shows an example of a distributed multi-agent reinforcement learning system. Only two agents are shown for simplicity, but the system can be extended to multiple agents. Each agent has multiple actors for sampling and multiple learners for model updating. These actors and learners can be processed in parallel to accelerate the training process. For details, see the A3C and IMPALA architectures described earlier. Trained models are uniformly stored and managed for symmetrical agents — if agents are asymmetrical, their models need to be stored separately. Models in the memory are scored by the model evaluator, which is a prerequisite for the model selector to work. Based on the output of the model evaluator — or meta-learner, such as policy space response oracle (PSRO) — and equilibrium solver, the model selector selects a model and distributes it to the actors of each agent. This process is known as league-based management . In terms of interaction with the environment, the distributed system uses an inference server to perform centralized inference on the model in each parallel process. To be specific, the inference server sends actions (based on observations) to the environment, which then performs parallel processing of these actions before returning observations, with the interaction trajectories collected and sent by the inference server to each agent for model training. While this example describes a distributed multi-agent system in general terms, there may be many different designs for different game types and algorithm structures in real-world applications.