12.5. Multi-agent Reinforcement Learning ¶
Previous sections discussed reinforcement learning involving only one agent. However, researchers are becoming increasingly interested in multiagent reinforcement learning. Consider the framework of single-agent reinforcement learning shown in Figure Fig. 12.2.1 . This framework considers the impact of only a single agent’s action on the environment, and the reward feedback from the environment applies only to this agent. If we extend the single-agent mode to multiple agents, we have at least two multiagent reinforcement learning frameworks, as shown in Figure Fig. 12.5.1 . Figure Fig. 12.5.1 (a) shows a scenario where multiple agents perform actions at the same time. The agents are unable to observe actions of other agents, and their actions have an overall impact on the environment. Each agent receives an individual reward for its actions. Figure Fig. 12.5.1 (b) shows a scenario where multiple agents perform actions in sequence. Each agent can observe the actions of its previous agents. Their actions have an overall impact on the environment. Each agent receives an individual or team reward. Aside from these two frameworks, other frameworks may involve a more complex mechanism of observations, communications, cooperation, and competition among agents. The simplest situation is to assume that the agent observations are the environment states. However, this is the least possible in the real world. In practice, agents usually have different observations on the environment.
Fig. 12.5.1 Two possible multiagent reinforcement learning frameworks: (a)Synchronous multiagent decision-making; (b) Asynchronous multiagentdecision-making ¶
12.5.1. Multi-agent RL ¶
Based on the Markov decision process used in single-agent reinforcement learning, we can define that used in multiagent reinforcement learning as a tuple \((\mathcal{S}, N, \boldsymbol{\mathcal{A}}, \mathbf{R}, \mathcal{T}, \gamma)\) . In the tuple, \(N\) indicates the number of agents, and \(\mathcal{S}\) and \(\boldsymbol{\mathcal{A}}=(\mathcal{A}_1, \mathcal{A}_2, ..., \mathcal{A}_N)\) are the environment state space and the multiagent action space, respectively, where \(A_i\) is the action space of the \(i\) th agent. \(\mathbf{R}=(R_1, R_2, ..., R_N)\) is the multiagent reward function. \(\mathbf{R}(s,\mathbf{a})\) : \(\mathcal{S}\times \boldsymbol{\mathcal{A}}\rightarrow \mathbb{R}^N\) denotes the reward vector with respect to the state \(s\in\mathcal{S}\) and multiagent action \(\mathbf{a}\in\boldsymbol{\mathcal{A}}\) , and \(R_i\) is the reward for the \(i\) th agent. The probability of transitioning from the current state and action to the next state is defined as \(\mathcal{T}(s^\prime|s,\mathbf{a})\) : \(\mathcal{S}\times\boldsymbol{\mathcal{A}}\times\mathcal{S}\rightarrow \mathbb{R}_+\) . \(\gamma\in (0,1)\) is the reward discount factor 1 . In addition to maximizing the expected cumulative reward \(\mathbb{E}[\sum_t \gamma^t r^i_t], i\in[N]\) for each agent, multiagent reinforcement learning involves other objectives such as reaching Nash equilibrium or maximizing the team reward — these do not form part of single-agent reinforcement learning.
We can therefore conclude that multiagent reinforcement learning is more complex than single-agent reinforcement learning, and that its complexity is not simply the accumulation of each agent’s decision complexity. Closely related to a classical research topic named Game theory, the research of multiagent systems has a long history — even before reinforcement learning became popular. There was significant research into such systems and many open theoretical problems existed. A typical one is that Nash equilibrium is unsolvable in a two-player non-zero-sum game 2 . We will not delve too deeply into such problems due to limited space. Instead, we will provide a simple example to explain why a multiagent learning problem cannot be directly solved using a single-agent reinforcement learning algorithm.
12.5.2. Game Example ¶
Consider the rock-paper-scissors game. In this game, the win-lose
relationship is scissors < rock < paper < scissors…
<
means that
the latter pure strategy wins over the previous one, and a reward of –1
or +1 is given to the two players, respectively. If both players choose
the same pure strategy, they are rewarded 0. The payoff table of the
game is provided in Table
Table 12.5.1
. The horizontal and
vertical headings indicate the strategies of Player 1 and Player 2,
respectively. The arrays in the table are the players’ rewards for their
actions.
|
Reward |
Scissors |
Rock |
Paper |
|---|---|---|---|
|
Scissors |
(0,0) |
(–1, +1) |
(+1, –1) |
|
Rock |
(+1, –1) |
(0,0) |
(–1, +1) |
|
Paper |
(–1, +1) |
(+1, –1) |
(0,0) |
Due to the antisymmetric nature of this matrix, the Nash equilibrium strategy is the same for both players, with a strategy distribution of \((\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\) . This means that both players have a \(\frac{1}{3}\) probability of choosing paper, rock, or scissors. If we treat the Nash equilibrium strategy as the objective of multiagent reinforcement learning, we can conclude that this strategy cannot be obtained simply through single-agent reinforcement learning. Assume that we randomly initialize two players for any two pure strategies. For example, Player 1 chooses scissors, and Player 2 chooses rock. Also assume that the strategy of Player 2 is fixed. As such, the strategy of Player 2 can be considered as a part of the environment. This allows us to use single-agent reinforcement learning to improve the strategy of Player 1 in order to maximize its reward. In this case, Player 1 converges to the pure strategy of paper. If we then fix this strategy for Player 1 to train Player 2, Player 2 converges to the pure strategy of scissors. In this way, Player 1 and Player 2 enter a cycle of three strategies, but neither of them can obtain the correct Nash equilibrium strategy.
12.5.3. Self-play ¶
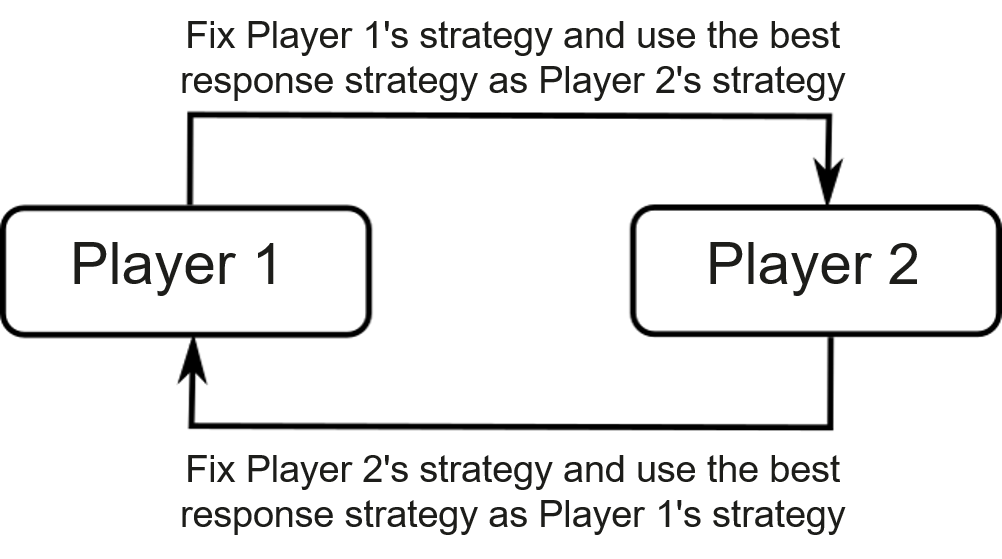
The learning method used in the preceding example is called self-play , as shown in Figure Fig. 12.5.2 . It is one of the most basic among the multiagent reinforcement learning methods. In self-play, given the fixed strategy of Player 1, the strategy of Player 2 is optimized by maximizing its own reward using single-agent learning methods. The strategy, referred to as best response strategy, is then fixed for Player 2 to optimize the strategy of Player 1. In this manner, the cycle repeats indefinitely. In some cases, however, self-play may fail to converge to the objective we expect. Due to the possible existence of such a cycle, we need training methods that are more complex and methods that are designed for multiagent learning to achieve our objective.
Generally, multiagent reinforcement learning is more complex than single-agent reinforcement learning. In self-play, a single-agent reinforcement learning process may be considered as a subtask of multi-agent reinforcement learning. In the game discussed above, when the strategy of Player 1 is fixed, Player 1 plus the game environment constitute the learning environment of Player 2, which can maximize its reward using single-agent reinforcement learning. Likewise, when the strategy of Player 2 is fixed, Player 1 can perform single-agent reinforcement learning. The cycle repeats indefinitely. This is why single-agent reinforcement learning can be considered as subtasks of multiagent reinforcement learning. Another learning method is fictitious self-play , as shown in Figure Fig. 12.5.3 , whereby an agent needs to choose an optimal strategy based on its opponent’s historical average strategies, and vice versa. In this manner, players can converge to Nash equilibrium strategy in games like rock-paper-scissors.