6.3. Operator Selection¶
Following graph optimization, the compiler backend generates a sequence of operators that can be executed on hardware. This is achieved by selecting the most suitable operators from a set of candidate operators for each node in the IR. Since these candidate operators have diverse specifications, their execution efficiency varies depending on the scenario. Therefore, the primary objective of operator selection is to choose the operators that are most appropriate for the target device based on the information provided by the IR.
6.3.1. Basic Concepts of Operator Selection¶
We can think of the nodes in a backend-optimized IR as being units of execution that are visible to the user, and each unit represents a hardware-agnostic operation in the user code. In essence, operator selection involves selecting appropriate hardware information, which is referred to as operator information. Such information defines the following:
The format of an operator, which is a determinant of the operator’s performance on the target platform. Machine learning systems commonly use NCHW and NHWC formats.
The data type (such as float32, float16, or int32) of an operator on the target platform. The operators selected are those with data types close to (or the same as) user definitions.
6.3.1.1. Data Formats¶
In machine learning systems, many operations are converted into matrix multiplication (e.g., convolution) for faster computation. Matrix multiplication in the form of \(\textit{\textit{A}}\times \textit{\textit{B}} = \textit{\textit{C}}\) is essentially a row-by-column multiplication. Specifically, the entry ij of C is obtained by multiplying the entries in the ith row of A and the corresponding entries in the jth column of B and then adding the results together. Consider the example shown in Figure Fig. 6.3.1. Matrix data is stored in row-major order by default, as shown at the top of the figure. However, matrix B is read in column-major order in the matrix multiplication process, as shown at the bottom.
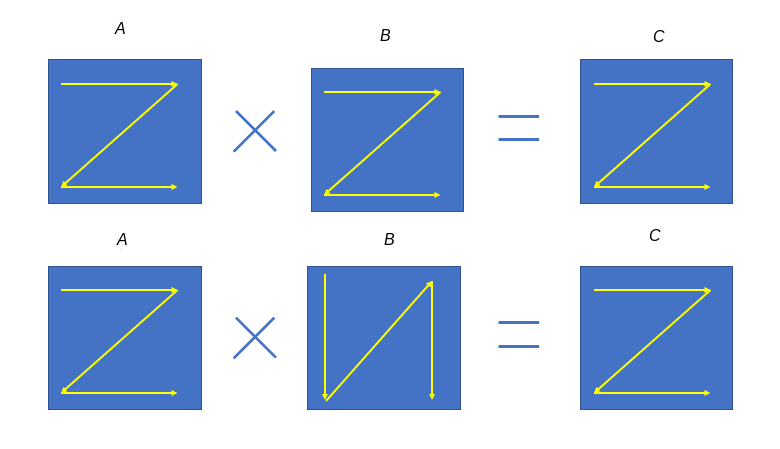
Fig. 6.3.1 Matrix data layouts in matrixmultiplication¶
Storing matrix B in the reading order increases the computation efficiency because access to contiguous blocks of memory is faster. We can therefore see that data formats play an important role in performance improvement.
There are two major formats in machine learning systems: NCHW and NHWC. For an image input, N denotes the batch size, C denotes the number of channels, and H and W denote the height and width respectively. Figure Fig. 6.3.2 depicts the logical diagram of an input with batch size 2, channels 16, height 5, and width 4.
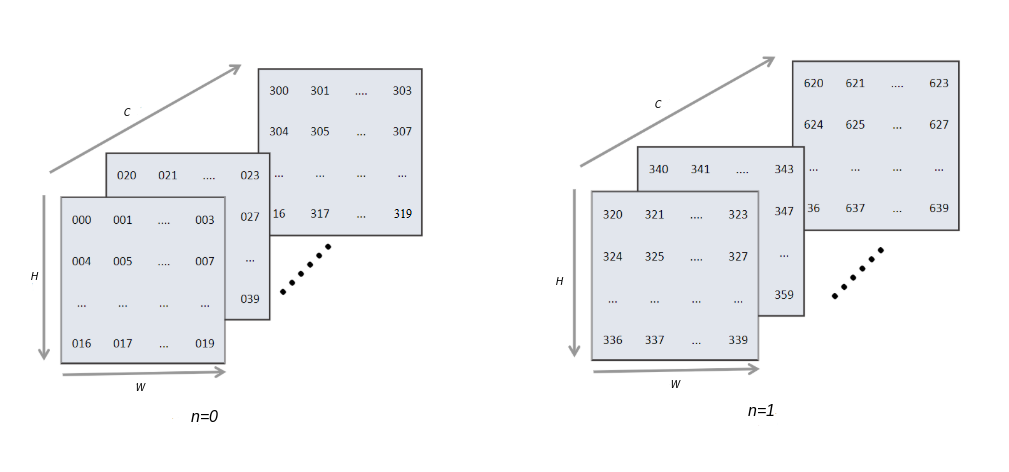
Fig. 6.3.2 Formatdiagram¶
A multidimensional matrix is flattened into 1D format before it is written to memory. This involves indexing, which maps logical data to physical memory.
Access to machine learning data is performed in an axis-wise order from
the last axis forward. For instance, data in NCHW format is read in the
axis order of W, H, C, and N. Equation ch05/equation-01
denotes the mapping between logical memory and physical memory for this
format of data.
:eqlabel:equation:ch05/equation-01
As shown in Figure Fig. 6.3.3, matrix elements are flattened from the lowest dimension (i.e., W axis) forward, and neighboring elements of an axis reside next to each other in memory. To take the same element on the next image in the same location, the whole image size (\(C*H*W\)) has to be jumped. Assume we have a batch of eight RGB images of size 32\(\times\)32, or a matrix with \(N=8,C=3,H=32,W=32\). Memory storage of these images begins from the first channel of the first image by flattening the matrix along axis W and then arranging matrix elements along axis H. This is performed before the next channel is processed. The same procedure is repeated until the last channel of the last image is processed. NCHW is the default format on PyTorch and MindSpore.
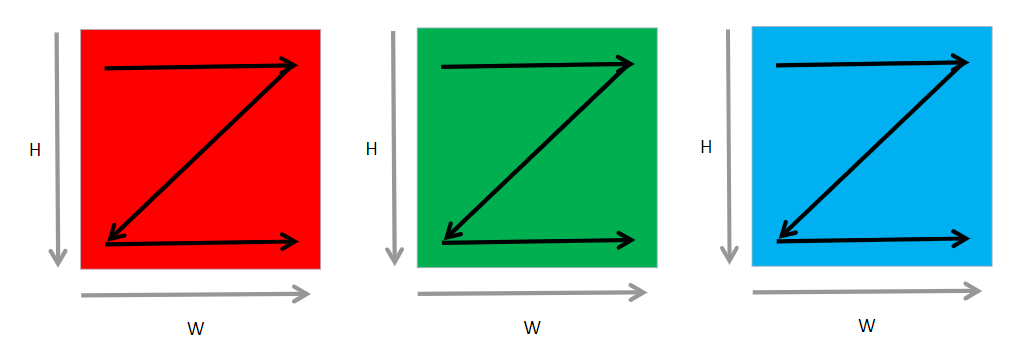
Fig. 6.3.3 RGB image data in NHWCformat¶
Access to data in NHWC format also begins at the lowest dimension (i.e.,
C axis) forward. NHWC is the default format on TensorFlow (PyTorch
refers to it as the channel-last format). Equation
ch05/equation-02 denotes the mapping from logical memory to
physical memory for this format of data.
:eqlabel:equation:ch05/equation-02
Figure Fig. 6.3.4 compares the logical indexing of the NCHW and NHWC formats. The [x:1] marks refer to the jumps from the innermost axis to the next. For example, [a:1] indicates the jump from axis W to axis H, and [b:1] indicates the jump from axis C (the innermost) to axis W.
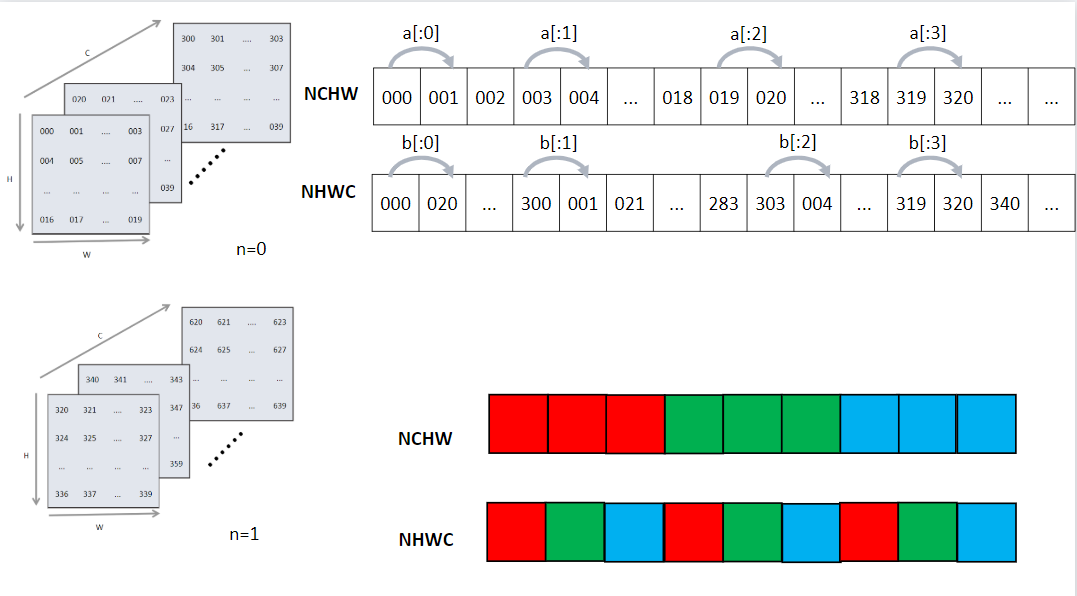
Fig. 6.3.4 NCHW and NHWCformats¶
These two formats offer a high degree of flexibility and are therefore used on many frameworks. However, to accelerate computing on hardware, further optimization is needed. In a machine learning system, if the size of the user input exceeds what the compute component can pass through the network at a time (which is often the case), the input will be batched before computation. For further optimization, many frameworks introduce blocked formats (which are more hardware-friendly), such as the nChw16c and nChw8c formats of the oneAPI Deep Neural Network Library (oneDNN) and the NC1HWC0 format on the Ascend platform. By leveraging hardware acceleration instructions to move and compute data, matrices can be quickly transformed into vectors, increasing the utilization of the on-chip cache.
6.3.1.2. Data Types¶
Single-precision (float32), occupying 32 bits in memory, is the most commonly used data type in machine learning systems. In applications where higher precision is not essential, the half-precision (float16) data type may be used, occupying 16 bits in memory. When used on hardware, float16 offers up to 7 times more arithmetic throughput with less memory footprint compared with the single-precision data type — this allows for larger batch sizes and consequently reduced training time. Next, we will look at the differences between half-precision floating-point numbers and single-precision floating-point numbers.
In Figure Fig. 6.3.5, Sig refers to the sign bit that indicates the sign of a number, Exponent refers to the exponent bits, and Mantissa refers to the mantissa bits.

Fig. 6.3.5 Binary representation of floating-pointnumbers¶
Applying Equation ch05/equation-03 will convert a float16
number in binary scientific notation to decimal format.
:eqlabel:equation:ch05/equation-03
If the exponent bits and mantissa bits are all 0s, the number is 0. If the exponent bits are all 0s but the mantissa bits are not, the number is very small. If the exponent bits are all 1s and the mantissa bits are all 0s, the number is an infinity, either positive or negative depending on the sign bit. Not a Number (NaN) is denoted by the exponent bits being all 1s while the mantissa bits are not all 0s. bfloat16 is a special data type developed by Google for machine learning on its tensor processing units (TPUs). Although bfloat16 is not an industry-standard IEEE 16-bit floating-point data type, it has the same exponent size as float32, meaning that it can be easily converted to and from float32.
6.3.1.3. Operator Information Library¶
Hardware devices support different operators based on their data format and data type requirements. Each device maintains an operator information library that contains a comprehensive list of operators supported by that device. During the operator selection process, the most suitable operators are chosen from this library. The library serves as a reference for determining which operators are compatible and can be efficiently executed on a particular hardware device.
6.3.2. Process of Operator Selection¶
Operator selection involves selecting the most appropriate operator for each operation node in an IR. Operator information contains the supported device type, data type, and data format. After the compiler frontend completes type inference and static analysis, the data type of user code is derived from the IR.
Figure Fig. 6.3.6 shows the operator selection process. First, the target hardware needs to be selected (or this step can be skipped in order to keep the default hardware selection defined in the compiler backend). The implementation, supported data types, and execution efficiency of a given operator vary depending on the target hardware. Then, the compiler backend selects an operator based on the data type and data format derived from the IR.
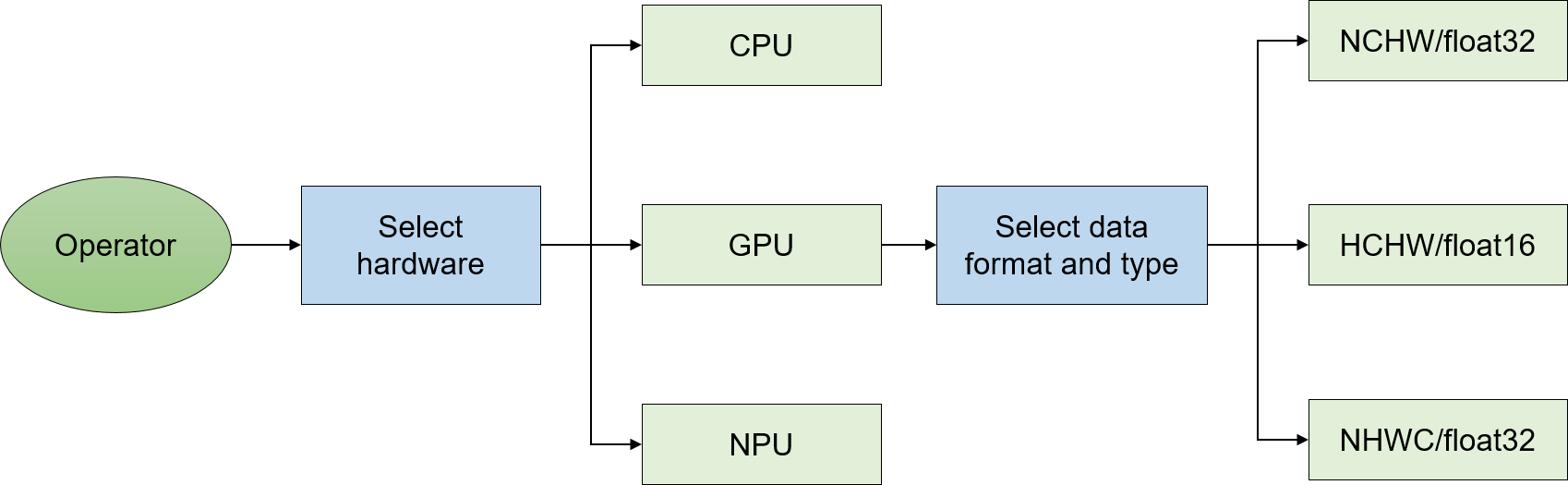
Fig. 6.3.6 Operator selection process (using GPU as anexample)¶
The result of the operator selection process might not be as expected due to software or hardware specifications. Sometimes, we might need to adjust the precision of a particular node to find an operator with the right data type. For example, the Conv2D operator supported by Ascend (i.e., the backend of MindSpore) allows only the float16 data type. When used on a float32 network on Ascend, the Conv2D operator is executable only when its input precision is reduced from float32 to float16.
Converting operators from one format to another can be time-consuming and incur memory movement overheads. To avoid this, data should be transferred between operators of the same format whenever possible. In addition, data type inconsistency may lead to reduced precision, potentially slowing down or even preventing network convergence. As such, thorough operator analysis is needed to ensure that the right data type is selected.
Simply put, an operator selection algorithm is considered optimal if it keeps the data type as consistent as possible with user settings while also minimizing data format conversion.
