5.3. Intermediate Representation

In this section, we begin by introducing basic IR concepts and the types of IR employed in classical compilers. Next, we address the new requirements and challenges that arise in the IR design for machine learning frameworks. To conclude this section, we examine the types of IRs utilized by well-known machine learning frameworks and delve into their implementation.

5.3.1. Definition of Intermediate Representations

An IR is a data structure or a form of code that a compiler utilizes to represent source code. Almost all compilers need IRs to model the program code that requires analysis, transformation, and optimization. The representational capability of an IR is crucial during the compilation process. It must accurately depict source code without information loss, ensure the completeness of the source-to-target code compilation, and guarantee the effectiveness and performance of code optimization.

As illustrated in Figure :numref:ch04/ch04-IR, IRs facilitate the representation of multiple source program languages from the frontend and enable the backend to connect to various target machines. Located between the frontend and backend is an optimizer, which allows for the addition of new optimization processes directly into the frontend and backend. These processes use existing IRs as input and generate new IRs as output. By analyzing and optimizing IRs, the optimizer enhances the extensibility of the compilation process and minimizes the impact that might be introduced during an optimization process on the frontend and backend.

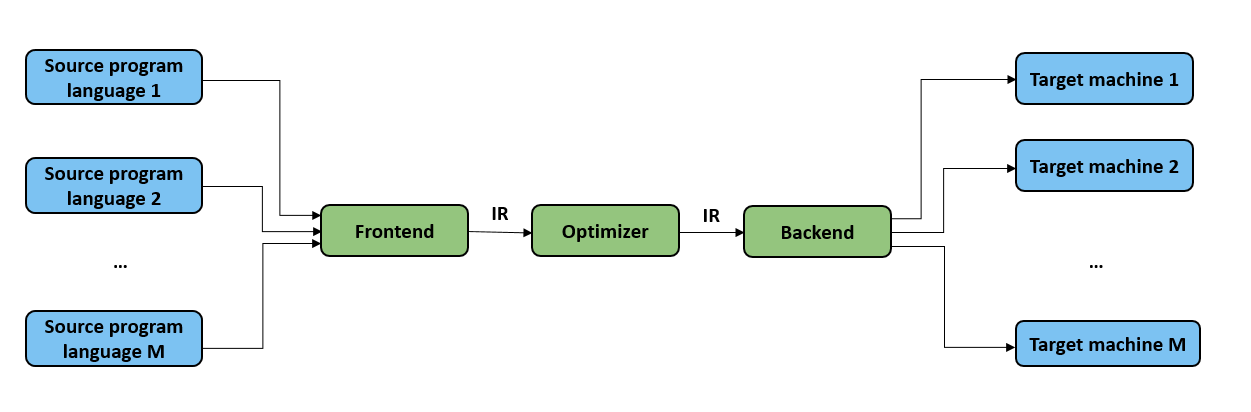
Fig. 5.3.1 Compiler’s optimizationprocess

With the ongoing evolution of compiler techniques, the development of IRs has progressed through three stages. In the initial stage, IRs were confined within a compiler and exclusively used by compiler developers. During the middle stage, when specific compilers became open source, IRs started being made publicly available, primarily for use by the users of compilers and related compilation tools. In the current stage, IRs are advancing toward facilitating an ecosystem of ecosystems (through a unified IR approach), encouraging increasing stakeholders (for example, hardware accelerator designers, machine learning framework users, and more) to participate in advertising AI computing.

5.3.2. Types of Intermediate Representations

We will discuss various types of IR structures used by classical compilers. Understanding these IR structures is essential for analyzing source programs and generating optimized compiled code. Table ch06/ch06-categorize offers an overview of the different IR types. It is important to design IR structures carefully, considering the specific requirements of the compiler’s design.

5.3.2.1. Linear Intermediate Representation

Linear IRs are widely used in compiler design, resembling assembly code for abstract machines. They represent the code to be compiled as a sequentially ordered series of operations. This ordering is important in practical terms. Linear IRs are popular because most processors utilize linear assembly languages.

Two common types of linear IRs are stack machine code and three-address code . Stack machine code, a form of single-address code, offers a straightforward and compact representation. Instructions in stack machine code typically consist solely of an opcode that specifies an operation, with operands stored on a stack. Most instructions retrieve operands from the stack and push the results of their operations back onto it. On the other hand, three-address code (3AC) emulates the instruction format used in modern RISC machines. It employs a set of quadruples, each containing an operator and three addresses (two operands and one target). Figure Fig. 5.3.2 illustrates the stack machine code and three-address code representations for the expression $a-b\ast 5$.

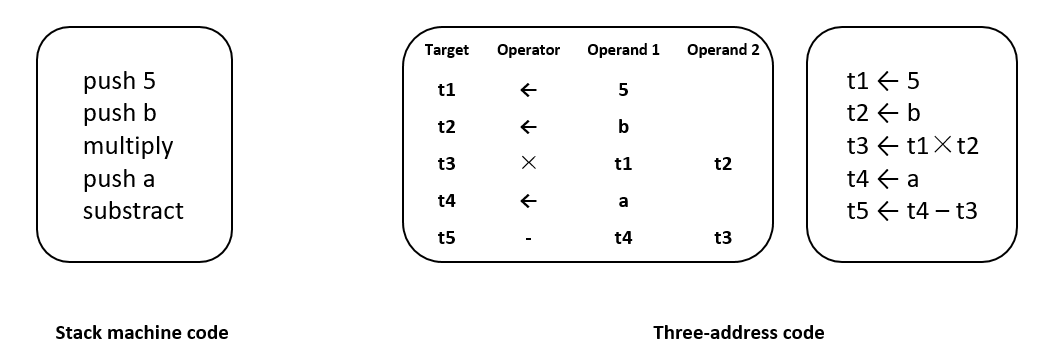
Fig. 5.3.2 Stack machine code and three-addresscode

5.3.2.2. Graphical Intermediate Representation

Graphical IRs store information about the compilation process in the form of graphs. These graphs utilize nodes, edges, lists, trees, and other elements to collectively represent an algorithm. Although all graphical IRs consist of nodes and edges, they differ in terms of abstraction levels and graph structures. Common examples of graphical IRs include abstract syntax trees (ASTs), directed acyclic graphs (DAGs), and control-flow graphs (CFGs).

An AST is a tree-structured IR that closely resembles the structure of the source code. Figure :numref:ch04/ch04-AST_DAG depicts the AST for the expression $a5+a5b$. It is worth noting that the AST contains two identical copies of $a5$, which introduces redundancy. To address this redundancy, the DAG offers a simplified representation where identical subtrees can be shared by multiple parent nodes. By reusing subtrees, the DAG reduces the cost of the evaluation process, especially when the compiler can verify that the value of $a$ remains constant.

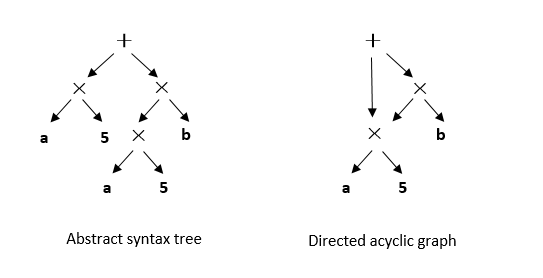
Fig. 5.3.3 AST and DAG

5.3.2.3. Hybrid Intermediate Representation

Hybrid IRs combine both linear IR and graphical IR elements. An example of a hybrid IR is LLVM IR , which is illustrated in Figure Fig. 5.3.4. LLVM is an open-source compiler framework with the goal of providing unified IRs for different frontends and backends.

In LLVM IR, linear IRs are used to construct basic blocks, while graphical IRs represent the control flow between these blocks. Each instruction within a basic block is presented as a static single assignment (SSA) . SSA requires each variable to be defined before use, with values assigned to them only once. Multiple SSA instructions form a linear list within a basic block.

In the control flow graph (CFG), each node represents a basic block, and control transfer between these blocks is implemented through edges. This combination of linear IR for basic blocks and graphical IR for control flow allows for a flexible and efficient representation in LLVM IR.

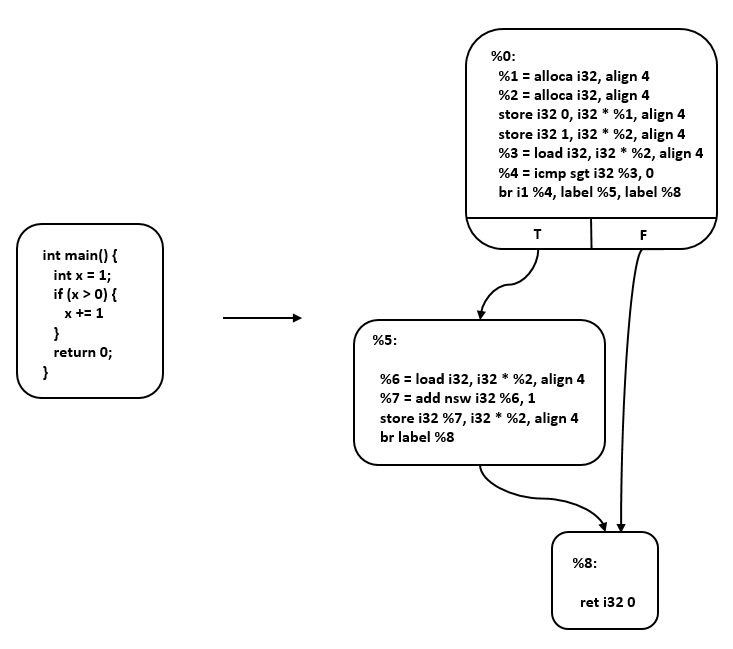
Fig. 5.3.4 LLVM IR

5.3.3. Intermediate Representation in Machine Learning Frameworks

Classical IRs (such as LLVM IR) primarily target programming languages for general-purpose computation tasks, which falls short of satisfying the unique requirements of machine-learning-related computation. When designing IRs tailored for machine learning frameworks, certain vital factors warrant attention:

• Tensor Representation. Given the predominance of tensor data in machine learning frameworks, it’s imperative that the IRs can effectively handle tensor representation.

• Automatic Differentiation. A core aspect of machine learning involves evaluating derivatives of neural networks and optimizers through automatic differentiation. Accordingly, IRs must prioritize simplicity, performance, and scalability of higher-order differentials for automatic differentiation.

• Computational Graph Mode. Machine learning frameworks like TensorFlow, PyTorch, and MindSpore operate on two computational graph modes: static and dynamic. The static mode, with pre-defined computational graphs, enhances optimization but compromises on flexibility. Conversely, the dynamic mode trades running speed for flexibility and easier debugging by executing operators immediately in the computational graph. IRs should therefore support both modes, enabling users to choose the one best suited for their tasks while building algorithm models.

• Support for Higher-order Functions and Closures. Essential in functional programming, higher-order functions take or return functions, while closures bundle code blocks with references to the surrounding environment, facilitating access to an outer function’s scope from an inner function. Such support reduces redundant code, improves abstraction, and enhances the flexibility and simplicity of framework representations.

• Compilation Optimization. Machine learning frameworks lean on compilation optimizations, including hardware-agnostic, hardware-specific, and deployment- or inference-related optimizations. These rely significantly on IRs implementations.

• Just-in-Time (JIT) Compilation. For expedited compilation and execution in machine learning frameworks, JIT compilation is frequently utilized. Optimization of JIT compilation, including loop unrolling, fusion, and inlining, plays a crucial role in optimizing parts of data flow graphs in IRs. A flawed IR design could potentially hamper JIT compilation performance in machine learning frameworks, thereby impacting the program’s running capabilities.

Considering these factors, developers persistently refine classical IRs and introduce new IRs specifically tailored for machine learning frameworks. In the following section, we will delve into the IRs employed by various machine learning frameworks.

5.3.3.1. Intermediate Representation in PyTorch

PyTorch is a dynamic, Python-oriented machine learning framework. Renowned for its usability and flexibility, PyTorch simplifies the process of writing and debugging machine learning programs. It introduces TorchScript, a method used for constructing serializable and optimizable models during the saving and loading of neural networks.

Particularly, TorchScript IR employs JIT compilation to convert Python code into target model files. All TorchScript programs can be saved within the Python process and later loaded into processes devoid of Python dependencies.

Aligning with the imperative programming paradigm, PyTorch incorporates the TorchScript IR, composed primarily of Single Static Assignment (SSA)-based linear IRs, to represent Python code. This representation can be achieved through either the Tracing or Scripting method of JIT compilation. TorchScript IR not only amplifies model deployment capabilities but also bolsters compilation performance. Additionally, TorchScript IR greatly improves the model visualization within the PyTorch framework.

Code lst:torchscript illustrates the use of the Scripting method to print a TorchScript IR graph.

lst:torchscript

import torch

    @torch.jit.script
    def test_func(input):
    rv = 10.0
    for i in range(5):
    rv = rv + input
    rv = rv/2
    return rv

    print(test_func.graph)

Code lst:torchscriptir shows the structure of this IR graph.

lst:torchscriptir

graph(%input.1 : Tensor):
    %9 : int = prim::Constant[value=1]()
    %5 : bool = prim::Constant[value=1]() # test.py:6:1
    %rv.1 : float = prim::Constant[value=10.]() # test.py:5:6
    %2 : int = prim::Constant[value=5]() # test.py:6:16
    %14 : int = prim::Constant[value=2]() # test.py:8:10
    %rv : float = prim::Loop(%2, %5, %rv.1) # test.py:6:1
    block0(%i : int, %rv.9 : float):
    %rv.3 : Tensor = aten::add(%input.1, %rv.9, %9) # <string>:5:9
    %12 : float = aten::FloatImplicit(%rv.3) # test.py:7:2
    %rv.6 : float = aten::div(%12, %14) # test.py:8:7
    -> (%5, %rv.6)
    return (%rv)

5.3.3.2. Intermediate Representation in JAX

The JAX framework facilitates both static and dynamic computational graphs and employs the Jax Program Representation (Jaxpr) IR. This IR ensures that the output, not reliant on global variables, depends solely on the input, with both input and output encapsulating typed information. Functionality-wise, Jaxpr IR supports an array of features such as loops, branching, recursion, closure function differentiation, third-order differentiation, as well as backpropagation and forward propagation in automatic differentiation.

Jaxpr IR utilizes the A-normal Form (ANF), a form of functional expression, demonstrated in Code lst:ANF via the ANF grammar.

lst:ANF

<aexp> ::=  NUMBER | STRING | VAR | BOOLEAN | PRIMOP
    |  (lambda (VAR ...) <exp>)
    <cexp> ::=  (<aexp> <aexp> ...)
    | (if <aexp> <exp> <exp>)
    <exp> ::=  (let ([VAR <cexp>]) <exp>) | <cexp> | <aexp>

The ANF segregates expressions into atomic expressions (aexp) and compound expressions (cexp). Atomic expressions represent constants, variables, primitives, and anonymous functions, while compound expressions, comprising several atomic expressions, can be viewed as invocations of anonymous or primitive functions. The first input in a cexp represents the invoked function, and all subsequent inputs symbolize the invoked parameters.

Code lst:JaxCode displays the Jaxpr corresponding to a function.

lst:JaxCode

from jax import make_jaxpr
    import jax.numpy as jnp

    def test_func(x, y):
    ret = x + jnp.sin(y) * 3
    return jnp.sum(ret)

    print(make_jaxpr(test_func)(jnp.zeros(8), jnp.ones(8)))

The structure of this Jaxpr is shown in Code lst:JaxPr.

lst:JaxPr

{ lambda ; a:f32[8] b:f32[8]. let
        c:f32[8] = sin b
        d:f32[8] = mul c 3.0
        e:f32[8] = add a d
        f:f32[] = reduce_sum[axes=(0,)] e
        in (f,) }

5.3.3.3. Intermediate Representation in TensorFlow

TensorFlow utilizes dataflow programming to execute numerical computations through dataflow graphs. TensorFlow’s static graph mechanism progresses through a series of abstractions and analyses when running a program, transforming it from higher-level to lower-level IRs, a process referred to as “lowering”.

To cater to diverse hardware platforms, TensorFlow employs a range of IR designs. As illustrated in Figure :numref:ch04/ch04-tensorflow_ecosystem, the blue boxes denote graph-based IRs while the green ones indicate SSA-based IRs. During the IR transformation, each level optimizes the IR independently, precluding communication with other levels. This absence of awareness about optimizations performed at other levels necessitates optimal implementation at each level, often leading to repetitive tasks and sub-optimal efficiency. Notably, transitioning from graph-based IRs to SSA-based IRs involves a qualitative transformation that incurs significant costs. The inability to reuse the same optimization code across levels also hampers development efficiency.

Multi-level IRs present a mixed bag of advantages and disadvantages. On the plus side, they offer flexible representations, pass-based optimization at varying levels, and efficient optimization algorithms. On the downside, they pose challenges due to their inherent characteristics: The transformation between different IRs often complicates full compatibility implementation, thereby increasing engineering workload and potentially leading to information loss. This might make lower-level optimization challenging if information at a higher level has been optimized. To mitigate such information loss, we can impose stricter constraints on the optimization sequence. Additionally, choosing the level for implementing certain optimizations that can be performed at two adjacent levels can be a conundrum for framework developers. Finally, defining distinct operator granularities at different levels might impact accuracy to a certain degree.

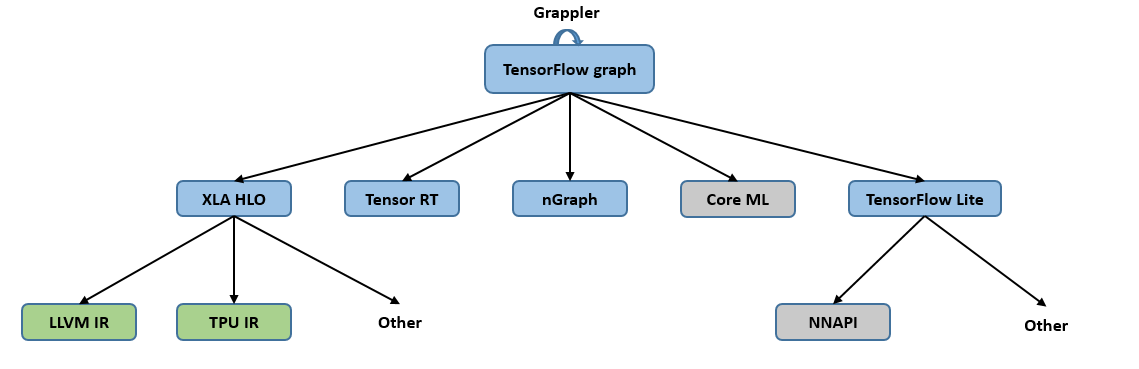
Fig. 5.3.5 TensorFlow’s IRdesign

5.3.3.4. Multi-Level Intermediate Representation

Multi-Level Intermediate Representation (MLIR) serves as a unified platform for IRs rather than being a specific type of IR. Leveraging the infrastructure provided by MLIR, developers can define IRs to suit their needs. Thus, MLIR can be interpreted as a “compiler of compilers”. It expands beyond the TensorFlow framework and can be used to construct IRs linking other languages to backend platforms (such as LLVM).

Despite the design of MLIR being heavily influenced by LLVM, MLIR fosters a more open ecosystem. Given that MLIR does not confine developers to a set group of operation or abstraction types, it offers more latitude to define IRs and solve specific problems. To facilitate this extensibility, MLIR introduces the concept of “dialects”. These provide a grouping mechanism for abstraction under a unique namespace. Each dialect lays out a production and associates an operation to an IR, thus producing an MLIR-typed IR. Within MLIR, the “operation” is the fundamental unit of abstraction and computation. Operations can carry application-specific semantics and encapsulate all the core IR structures in LLVM, including instructions, functions, modules, etc.

The MLIR assembly for an operation is illustrated as follows:

%tensor = "toy.transpose"(%tensor) {inplace = true} : (tensor<2x3xf64>) -> tensor<3x2xf64> loc("example/file/path":12:1)

This MLIR operation can be dissected as follows:

• %tensor: The identifier for the result defined by this operation (prefixed with a $\mathrm{\%}$ to prevent naming conflicts). An operation may define no results or multiple results, represented as SSA values.

• “toy.transpose”: The operation name. It is usually a unique string, with the dialect’s namespace prefixing the “.”. This refers to the transpose operation within the toy dialect.

• (%tensor): A list that can contain zero or more input operands (or arguments), which are SSA values defined by other operations or that refer to block arguments.

• inplace = true: A dictionary that may contain zero or more attributes. These are constant special operands. Here, a boolean attribute named inplace with a constant value of true is defined.

• (tensor<2x3xf64>)->tensor<3x2xf64>: This represents the operation type in a functional form, specifying the input before the arrow and output after. The data types and shapes of the input and output are contained within the parentheses. For instance, $<2x3xf64>$ represents a tensor with a shape of (2, 3) and data type float64.

• loc(“example/file/path”:12:1): This refers to the source code location from where this operation originated.

As each level’s IR design adheres to this assembly, it simplifies transformation across levels, boosting the efficiency of IR transformation. Moreover, different levels can interact to optimize the IRs, enabling optimization to be performed at the most suitable level, thereby negating the need for optimal performance at each level. By transforming them into the IR at the most appropriate level, other IRs can be optimized, enhancing both optimization and development efficiency. TensorFlow can also employ MLIR to perform multi-layer transformation from graph-based IRs to

5.3.3.5. Intermediate Representation in MindSpore

MindSpore adopts graph-based functional IRs, known as MindSpore IR (abbreviated to MindIR). MindIR employs a unified IR approach instead of a multi-level IR structure, outlining the network’s logical structure and operator attributes. This approach obliterates model disparities across different backends, facilitating connections to various target machines.

MindIR primarily caters to the automatic differential transformation. It implements a transformation method grounded in functional programming frameworks, thereby making it similar to ANF (A-Normal Form) functional semantics. Its defining characteristics include:

1. Graph-based Representation. MindSpore represents programs as graphs which are conducive to optimization. MindSpore treats functions as essential elements of a machine learning program, allowing for recursive invocation, parameter passing, or returning from other functions. This ability paves the way for representing a range of control flow structures.

2. Purely Functional. In a purely functional context, the function outcomes depend solely on parameters. Side effects are potential issues when a function relies on or affects external states, such as global variables. These can lead to incorrect results if code execution sequence isn’t strictly maintained. These side effects can also impact automatic differentiation, necessitating the requirement for pure functions. MindIR has the capability to transform representations with side effects into purely functional representations, ensuring correct code execution sequence while upholding ANF functional semantics and enabling a higher degree of automatic differentiation freedom.

3. Closure Representation. Reverse mode automatic differentiation requires the storage of basic operation intermediate results in closures for a combined connection. Closures, the combination of a code block bundled with references to its surrounding environment, become particularly crucial. In MindIR, the code block takes the shape of a function diagram, with the surrounding environment interpreted as the function invocation context.

4. Strongly Typed. Each node requires a specific type for achieving optimal performance. This is particularly crucial in machine learning frameworks where operator execution can be time-consuming. Detecting errors at the earliest can help save valuable time. MindIR’s type and shape inference capabilities thus center on the support for function invocation and higher-order functions.

Figure :numref:ch04/ch04-MindIR outlines the MindIR grammar based on MindSpore framework’s characteristics. ANode corresponds to an atomic expression in ANF, ValueNode represents the constant value, ParameterNode signifies the function’s formal parameter, and CNode (corresponding to a compound expression in ANF) indicates function invocation.

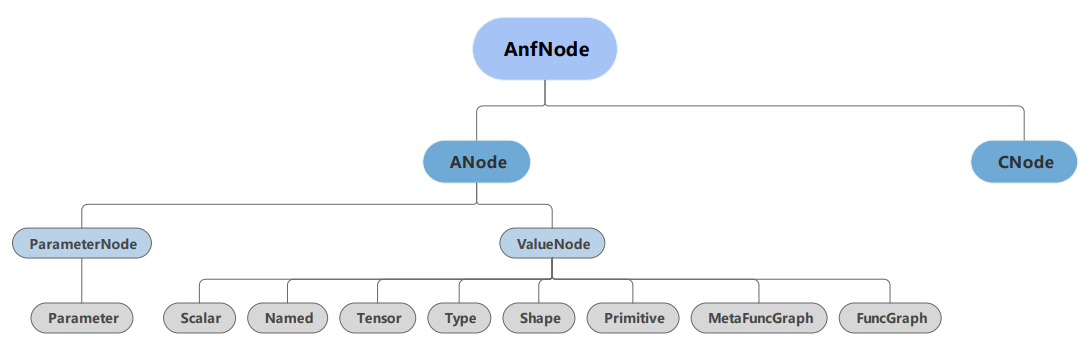
Fig. 5.3.6 MindIR grammar

The example provided below in Code 1 offers a deeper analysis of MindIR.

lst:MindSporeCode

def func(x, y):
    return x / y

    @ms_function
    def test_f(x, y):
    a = x - 1
    b = a + y
    c = b * func(a, b)
    return c

The ANF expression corresponding to this function is demonstrated in Code lst:MindIR.

lst:MindIR

lambda (x, y)
    let a = x - 1 in
    let b = a + y in
    let func = lambda (x, y)
    let ret = x / y in
    ret end in
    let %1 = func(a, b) in
    let c = b * %1 in
    c end

In ANF, each expression is encapsulated as a variable utilizing the let expression, with dependencies on the expression’s output represented via variable references. In contrast, MindIR packages each expression as a node, portraying dependencies through directed edges connecting the nodes.